Expression d'une série entière avec des fonctions usuelles


Colle de mathématiques

Sujet de colle de maths:

Énoncé du sujet

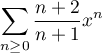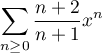On considère la série entière $\dsp\sum_{n\geq 0}\frac{n+2}{n+1}x^n$.
Donner son rayon de convergence et l'exprimer en termes de fonctions usuelles.


Correction

Correction

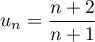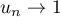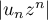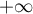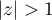Soit $u_n=\dfrac{n+2}{n+1}$. Puisque $u_n\to 1$, la suite $|u_nz^n|$ est bornée si $|z|<1$ et tend vers $+\infty$ si $|z|>1$. Le rayon de convergence de la série est donc égal à 1.

Pour sommer la série entière, on décompose en éléments simples:
\[\frac{n+2}{n+1}=1+\frac{1}{n+1}\]

ce qui donne
\[\begin{array}{lcl} \dsp\sum_{n\geq 0}\frac{n+2}{n+1}x^n&=&\dsp\sum_{n\geq 0}x^n+\sum_{n\geq 0}\frac{1}{n+1}x^n\\[.6em] &=&\dfrac{1}{1-x}+\dfrac1x\dsp\sum_{n\geq 0}\frac{x^{n+1}}{n+1}\\[.6em] &=&\dfrac{1}{1-x}-\dfrac{\ln(1-x)}{x}. \enar\]



Tag:Séries entières

Autres sujets au hasard: Lancer de dés

Voir aussi:
LongPage: h2: 3 - h3: 0