Détermination d'une limite
Colle de mathématiques
Sujet de colle de maths:- LimiteLimites de suites et de fonctions
Énoncé du sujet
Déterminer la limite en 0 de
,
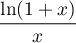et en déduire celle de
,
et en déduire celle de
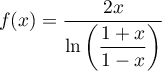
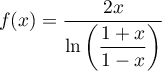
Correction
![\[\dfrac{\ln(1+x)}{x}=\dfrac{\ln(1+x)-\ln(1)}{(1+x)-1}\]](/Generateur-Devoirs/Colles/limites/ex8_c/1.png)
et donc, par définiton de la dérivée de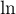
en 1,
![\[\lim_{x\to0}\dfrac{\ln(1+x)}{x}=\ln'(1)=\dfrac11=1\]](/Generateur-Devoirs/Colles/limites/ex8_c/3.png)
On a alors,
![\[\begin{array}{ll} f(x)
&=\dfrac{2x}{\ln\lp\dfrac{1+x}{1-x}\right)}\\[2.8em]
&=\dfrac{2x}{\ln(1+x)-\ln(1-x)}\\[1.5em]
&=\dfrac{2x}{x\lp\dfrac{\ln(1+x)}{x}-\dfrac{\ln(1-x)}{x}\right)}\\
&=\dfrac{2}{\dfrac{\ln(1+x)}{x}-\dfrac{\ln(1-x)}{x}}
\enar\]](/Generateur-Devoirs/Colles/limites/ex8_c/4.png)
avec donc,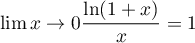
,
et de même,
,
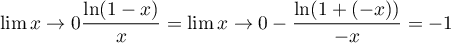on obtient finalement,
![\[\lim{x\to0}f(x)=\dfrac{2}{1-(-1)}=1\]](/Generateur-Devoirs/Colles/limites/ex8_c/7.png)
Correction
On aet donc, par définiton de la dérivée de
en 1,
On a alors,
avec donc,
,
et de même,
,
on obtient finalement,
Tag:Limite
Autres sujets au hasard:
Voir aussi: