Démonstration d'une propriété intégrale

Colle de mathématiques

Sujet de colle de maths:

IntégraleIntégrale

Énoncé du sujet

Montrer que pour toute fonction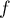

continue sur

on a

$\int_0^\pi xf\lp\sin x\rp\,dx=\pi\int_0^{\frac\pi2} f\lp\sin x\rp\,dx$

Correction

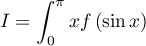Soit $I=\dsp\int_0^\pi xf\lp\sin x\rp$ .
Comme dans toutes les intégrales de l'égalité le terme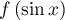 $f\lp\sin x\rp$ semble invariant, cela nous incite à trouver un changement de variable qui laisse effectivement invariant ce terme, donc invariant le sinus (n'ayant pas d'autre information sur

).
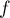On pose donc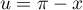 $u=\pi-x$ , et donc

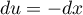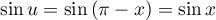et, comme justement $\sin u=\sin\lp\pi-x\rp=\sin x$ ,

$\begin{array}{ll} I&\dsp=-\int_\pi^0\lp\pi-u\right) f\lp\sin u\right)\,du\\ &=\dsp\int_0^\pi\lp\pi-u\right) f\lp\sin u\right)\,du \\ &=\dsp\pi\int_0^\pi f\lp\sin u\rp\,du-\int_0^\pi u f\lp\sin u\rp\,du\\ &=\dsp\pi\int_0^\pi f\lp\sin u\rp\,du-I\enar$

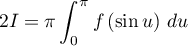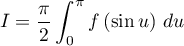On en déduit donc que $2I=\dsp\pi\int_0^\pi f\lp\sin u\rp\,du$ ou encore que $I=\dsp\dfrac\pi2\int_0^\pi f\lp\sin u\rp\,du$ .

Il reste maintenant à découper l'intervalle d'intégration pour arriver à l'égalité recherchée:

$\int_0^\pi f\lp\sin u\rp\,du =\int_0^{\frac\pi2} f\lp\sin u\rp\,du+\int_{\frac\pi2}^\pi f\lp\sin u\rp\,du$

et avec à nouveau le changement de variable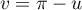 $v=\pi-u$ dans la dernière intégrale:

$\begin{array}{ll}\dsp\int_{\frac\pi2}^\pi f\lp\sin u\rp\,du&=\dsp-\int_{\frac\pi2}^0f\p\sin v\rp\,dv\\ &\dsp=\int_{\frac\pi2}^\pi f\lp\sin u\rp\,dv\enar$

et donc,

$\int_0^\pi f\lp\sin u\rp\,du=2\int_0^{\frac\pi2} f\lp\sin u\rp\,du$

d'où l'égalité recherchée:

$I=\dfrac\pi2\int_0^\pi f\lp\sin u\rp\,du=\pi\int_0^{\frac\pi2} f\lp\sin u\rp\,du$

Tag:Intégrale

Autres sujets au hasard:

Voir aussi: