Croissance bornée d' une fonction
Colle de mathématiques
Sujet de colle de maths:- Rolle - AFThéorème de Rolle et théorème des accroissements finis
Énoncé du sujet
Existe-t'il une fonction 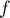 , définie et dérivable sur
, définie et dérivable sur ![$[0;2]$](/Generateur-Devoirs/Colles/Calcul/exAF3/2.png) ,
telle que
,
telle que  et
et 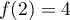 et de plus
et de plus 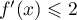 pour tout
pour tout 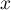 ?
?
Correction
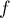 une telle fonction. Alors, il existe
une telle fonction. Alors, il existe ![$c\in]0;2[$](/Generateur-Devoirs/Colles/Calcul/exAF3_c/2.png) tel que
tel que
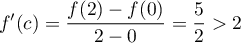 ,
ce qui est impossible.
,
ce qui est impossible.
Ainsi, il n'existe pas une telle fonction.
Correction
SoitAinsi, il n'existe pas une telle fonction.
Tag:Rolle - AF
Autres sujets au hasard:

Voir aussi: