Courbe paramétrée fractions rationnelles
Colle de mathématiques
Sujet de colle de maths:- Courbes paramétréesCourbes paramétrées
Énoncé du sujet
Soit 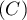 la courbe définie par la représentation paramétrique
la courbe définie par la représentation paramétrique
![$\la\begin{array}{ll}
x(s)=\dfrac{1}{1+s^2} \\[0.3cm]
y(s)=\dfrac{-s}{1+s^2}
\enar\right.$](/Generateur-Devoirs/Colles/courbesparam/ex4/2.png) ,
, 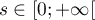 .
.
![$\la\begin{array}{ll}
x(s)=\dfrac{1}{1+s^2} \\[0.3cm]
y(s)=\dfrac{-s}{1+s^2}
\enar\right.$](/Generateur-Devoirs/Colles/courbesparam/ex4/2.png) ,
, - Calculer les dérivées des fonctions
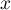 et
et 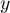 , puis établir le
tableau des variations conjointes de
, puis établir le
tableau des variations conjointes de 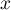 et
et 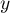 .
.
- On note
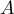 le point de la courbe lorsque
le point de la courbe lorsque  ,
et
,
et 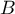 le point de la courbe lorsque
le point de la courbe lorsque  .
Déterminer les coordonnées des points
.
Déterminer les coordonnées des points 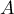 et
et 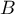 .
.
Préciser la direction de la tangente à la courbe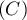 aux points
aux points
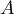 et
et 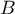 .
.
- Tracer alors, en utilisant tous les résultats précédents, la
courbe
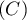 .
.
Correction
Correction
-
![$\la\begin{array}{ll}
x'(s)=\dfrac{-2s}{(1+s^2)^2} \\[0.3cm]
y'(s)=\dfrac{-(1+s^2)+2s^2}{(1+s^2)^2}
=\dfrac{s^2-1}{(1+s^2)^2}
\enar\right.$](/Generateur-Devoirs/Colles/courbesparam/ex4_c/1.png) d'où,
d'où,
![\[\begin{tabular}{|c|ccccc|}\hline
$s$ & $0$ && $1$ && $+\infty$ \\\hline
$x'(s)$ & $0$ & & $-$& & 0 \\\hline
&1&&&&\\
$x(s)$ && & \psline{->}(-1,0.5)(1.2,-0.2)
\rput(0,0){$\frac12$}& & \\
&&&&&0\\\hline
&0&&&&0\\
$y(s)$ && \psline{->}(-0.6,0.5)(0.6,-0.2)&
\psline{->}(0.2,-0.2)(1.4,0.4)& & \\
&&& $-\frac12$ &&\\\hline
$y'(s)$ & $-1$ & $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$& 0 \\\hline
\end{tabular}\]](/Generateur-Devoirs/Colles/courbesparam/ex4_c/2.png)
-
Lorsque
 ,
, 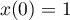 et
et 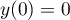 , d'où
, d'où 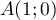 .
.
Lorsque ,
, 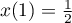 et
et 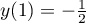 , d'où
, d'où
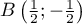 .
.
En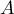 ,
, 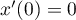 et
et 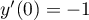 ; ainsi, la tangente en
; ainsi, la tangente en 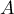 est
verticale.
est
verticale.
En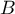 ,
, 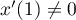 et
et 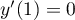 ; ainsi la tangente en
; ainsi la tangente en 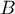 est
horizontale.
est
horizontale.
-
(0.5,-0.5)(0,-0.5)
\rput(0.5,0.1){$\frac12$}
\rput(-0.15,-0.5){$-\frac12$}
\psline{<->}(0.1,-0.5)(0.9,-0.5)
\psline{->}(0,0)(0,-0.7)
\parametricplot[plotpoints=1000,linecolor=red,linewidth=1.5pt]{0}{100}{
1 1 t 2 exp add div
-1 t mul 1 t 2 exp add div
}
\rput(1.06,-0.06){$A$}
\rput(0.5,-0.56){$B$}
\end{pspicture}\]](/Generateur-Devoirs/Colles/courbesparam/ex4_c/19.png)
Tag:Courbes paramétrées
Autres sujets au hasard:

Voir aussi: