Convergence d'une intégrale, IPP
Colle de mathématiques
Sujet de colle de maths:- IntégraleIntégrale
Énoncé du sujet
Montrer que l'intégrale 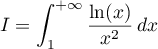 converge et calculer sa valeur.
converge et calculer sa valeur.
Correction
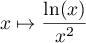 est continue sur
est continue sur  et l'intégrale existe sur tout segment
et l'intégrale existe sur tout segment ![$[1;A]$](/Generateur-Devoirs/Colles/Integrale/convergence-IPP_c/3.png) pour tout réel
pour tout réel 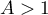 .
.
Il reste à étudier la convergence en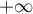 .
On a
.
On a
![\[\lim_{x\to+\infty}x^{3/2}\dfrac{\ln(x)}{x^2}
=\lim_{x\to+\infty}\dfrac{\ln(x)}{x^{1/2}}
=0\]](/Generateur-Devoirs/Colles/Integrale/convergence-IPP_c/6.png)
par croissances comparées, ce qui montre que
![\[\dfrac{\ln(x)}{x^2}=o\lp\dfrac1{x^{3/2}}\rp\]](/Generateur-Devoirs/Colles/Integrale/convergence-IPP_c/7.png)
et donc que l'intégrale est convergente en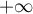 d'après le critère
de Riemann.
d'après le critère
de Riemann.
Pour calculer cette intégrale, on peut penser à une intégration par parties pour enlever le logarithme en le dérivant,
![\[\begin{array}{ll}I&=\dsp\int_1^{+\infty}\ln(x)\dfrac1{x^2}\,dx\\[1em]
&=\Bigl[\ln(x)\lp-\dfrac1x\rp\Bigr]_1^{+\infty}
-\dsp\int_1^{+\infty}\dfrac1x\lp-\dfrac1x\rp\,dx\\[1.2em]
&=0+\dsp\int_0^{+\infty}\dfrac1{x^2}\,dx
=\Bigl[-\dfrac1x\Bigr]_1^{+\infty}
=1
\enar\]](/Generateur-Devoirs/Colles/Integrale/convergence-IPP_c/9.png)
Correction
La fonctionIl reste à étudier la convergence en
par croissances comparées, ce qui montre que
et donc que l'intégrale est convergente en
Pour calculer cette intégrale, on peut penser à une intégration par parties pour enlever le logarithme en le dérivant,
![\[\begin{array}{ll}I&=\dsp\int_1^{+\infty}\ln(x)\dfrac1{x^2}\,dx\\[1em]
&=\Bigl[\ln(x)\lp-\dfrac1x\rp\Bigr]_1^{+\infty}
-\dsp\int_1^{+\infty}\dfrac1x\lp-\dfrac1x\rp\,dx\\[1.2em]
&=0+\dsp\int_0^{+\infty}\dfrac1{x^2}\,dx
=\Bigl[-\dfrac1x\Bigr]_1^{+\infty}
=1
\enar\]](/Generateur-Devoirs/Colles/Integrale/convergence-IPP_c/9.png)
Tag:Intégrale
Autres sujets au hasard:

Voir aussi: