Coefficients binomiaux, puissance n-ième et inverse
Colle de mathématiques
Sujet de colle de maths:- MatricesMatrices
Énoncé du sujet
Soit 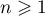 un entier naturel.
un entier naturel.
- Soit
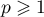 un entier.
Montrer que
un entier.
Montrer que 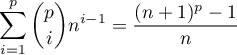 .
.
- Soit
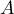 la matrice de
la matrice de 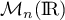 dont tous les coefficients valent 1.
Calculer
dont tous les coefficients valent 1.
Calculer 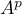 pour tout
pour tout 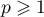 .
.
- Soit
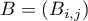 la matrice carrée de taille
la matrice carrée de taille 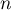 définie par
définie par
![\[b_{i,j}=\la\begin{array}{rcl}2&\text{ si } &i=j\\1&\text{ si } &i\not=j\enar\right.\]](/Generateur-Devoirs/Colles/matrices/puissance-inverse/10.png)
Calculer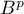 pour
pour 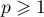 .
.
- Montrer que
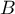 est inversible et calculer son inverse.
est inversible et calculer son inverse.
Correction
Correction
- En utilisant la formule du binôme de Newton, on a
![\[\begin{array}{ll}\dsp\sum_{i=1}^p\binom{p}{i}n^{i-1}
&=\dsp\dfrac1n\sum_{i=1}^p\binom{p}{i}n^i\\[1.5em]
&=\dsp\dfrac1n\lp\sum_{i=0}^p\binom{p}{i}n^i-1\rp\\[1.4em]
&=\dfrac1n\biggl((n+1)^p-1\biggr)\enar\]](/Generateur-Devoirs/Colles/matrices/puissance-inverse_c/1.png)
- On calcule
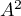 : tous ses coefficients sont égaux à
: tous ses coefficients sont égaux à 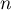 ,
c'est-à-dire que
,
c'est-à-dire que 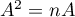 .
.
On a donc alors que
![\[A^3=A^2\,A=nA\,A=nA^2=n^2A\]](/Generateur-Devoirs/Colles/matrices/puissance-inverse_c/5.png)
puis, par une récurrence immédiate, pour tout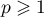 ,
,
![\[A^p=n^{p-1}A\]](/Generateur-Devoirs/Colles/matrices/puissance-inverse_c/7.png)
- On remarque que
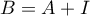 , où
, où 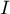 est la matrice identité de taille
est la matrice identité de taille 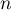 .
.
On a alors d'après la formue du binôme, comme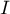 et
et 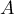 commutent, et d'après les questions précédentes,
commutent, et d'après les questions précédentes,
![\[\begin{array}{ll}B^p=(A+I)^p
&=\dsp\sum_{i=0}^p\binom{p}{i}A^iI^{p-i}\\[1.5em]
&=\dsp\sum_{i=1}^p\binom{p}{i}n^{i-1}A+I\\[1.5em]
&=\lp\dfrac{(n+1)^p-1}n\right) A +I
\enar\]](/Generateur-Devoirs/Colles/matrices/puissance-inverse_c/13.png)
- Pour montrer que
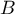 est inversible on pense bien sûr au déterminant (qui doit être non nul), mais cela ne donne pas directement l'inverse pour autant.
est inversible on pense bien sûr au déterminant (qui doit être non nul), mais cela ne donne pas directement l'inverse pour autant.
On peut ici plutôt revenir à la définition et tenter d'utiliser les résultats précédents.
On cherche une matrice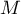 , qui commute avec
, qui commute avec 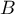 , telle que
, telle que
![\[BM=I\]](/Generateur-Devoirs/Colles/matrices/puissance-inverse_c/17.png)
Or,d'après la question précédente, on a
![\[B^p=\alpha_p A+I\]](/Generateur-Devoirs/Colles/matrices/puissance-inverse_c/18.png)
en notant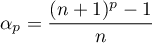 le coefficient de la première question.
le coefficient de la première question.
Comme , on a alors aussi
, on a alors aussi
![\[\begin{array}{ll}&B^p=\alpha_p(B-I)+I\\[.4em]
\iff& B^p-\alpha_pB=\lp1-\alpha_p\right) I\\[.4em]
\iff& B\left( B^{p-1}-\alpha_pI\rp=\left(1-\alpha_p\rp I\\[.4em]
\iff& BM=I\enar\]](/Generateur-Devoirs/Colles/matrices/puissance-inverse_c/21.png)
qui montre donc que est inversible, d'inverse
est inversible, d'inverse
![\[M=B^{-1}=\dfrac1{1-\alpha_p}\left( B^{p-1}-\alpha_pI\rp\]](/Generateur-Devoirs/Colles/matrices/puissance-inverse_c/23.png)
D'après l'unicité de la matrice inverse, on peut affirmer que l'expression précédente ne dépend pas de .
On peut donc choisir par exemple
.
On peut donc choisir par exemple  , ou chercher à aller plus loin généralement:
, ou chercher à aller plus loin généralement:
![\[B^{p-1}=\alpha_{p-1}A+I\]](/Generateur-Devoirs/Colles/matrices/puissance-inverse_c/26.png)
et donc
![\[\begin{array}{ll}B^{-1}&=\dfrac1{1-\alpha_p}\left( \alpha_{p-1}A+I-\alpha_pI\rp\\[1.2em]
&=\dfrac{\alpha_{p-1}}{1-\alpha_p}A+I
\enar\]](/Generateur-Devoirs/Colles/matrices/puissance-inverse_c/27.png)
puis, en utilisant l'expression du coefficient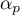 :
:
![\[\begin{array}{ll}B^{-1}&=\dfrac{(n+1)^{p-1}-1}{n-\lp(n+1)^p-1\right)}A+I\\[1.2em]
&=-\dfrac{(n+1)^{p-1}-1}{(n+1)^p-(n+1)}A+I\\[1em]
&=-\dfrac1{n+1}A+I
\enar\]](/Generateur-Devoirs/Colles/matrices/puissance-inverse_c/29.png)
Remarque: ces calculs poursuivent directement le résultat de la question 2. précédente.
On peut néanmoins trouver plus simple.
D'après les relations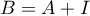 et
et 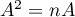 on a
on a
![\[\begin{array}{ll}BA&=(A+I)A\\
&=A^2+A\\
&=(n+1)A\\
&=(n+1)(B-I)
\enar\]](/Generateur-Devoirs/Colles/matrices/puissance-inverse_c/32.png)
d'où
![\[\begin{array}{ll}&B-\dfrac1{n+1}BA=I\\[.8em]
\iff&B\left( I-\dfrac1{n+1}A\rp=I\enar\]](/Generateur-Devoirs/Colles/matrices/puissance-inverse_c/33.png)
et on retrouve l'expression (et l'existence) de l'inverse de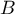 .
.
Tag:Matrices
Autres sujets au hasard:

Voir aussi: