Calcul matriciel - Inverse
Colle de mathématiques
Sujet de colle de maths:- MatricesMatrices
Énoncé du sujet
Soit 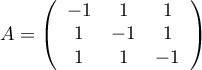 .
Montrer que
.
Montrer que 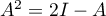 .
.
En déduire que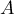 est inversible et calculer
est inversible et calculer 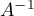 .
.
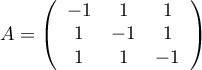 .
Montrer que
.
Montrer que En déduire que
Correction
![\[A^2=AA=
\lp\begin{array}{ccc}-1&1&1\\1&-1&1\\1&1&-1\enar\right)
\lp\begin{array}{ccc}-1&1&1\\1&-1&1\\1&1&-1\enar\right)
=\lp\begin{array}{ccc}3&-1&-1\\-1&3&-1\\-1&-1&3\enar\right)
=AI-A\]](/Generateur-Devoirs/Colles/matrices/ex1_c/1.png)
On a donc aussi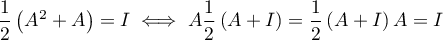 ,
,
ce qui montre que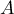 est inversible avec
est inversible avec 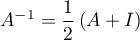 .
.
Correction
On trouve bien que![\[A^2=AA=
\lp\begin{array}{ccc}-1&1&1\\1&-1&1\\1&1&-1\enar\right)
\lp\begin{array}{ccc}-1&1&1\\1&-1&1\\1&1&-1\enar\right)
=\lp\begin{array}{ccc}3&-1&-1\\-1&3&-1\\-1&-1&3\enar\right)
=AI-A\]](/Generateur-Devoirs/Colles/matrices/ex1_c/1.png)
On a donc aussi
ce qui montre que
Tag:Matrices
Autres sujets au hasard:

Voir aussi: