Cauchy-Schwarz et une application
Colle de mathématiques
Sujet de colle de maths:- Espaces euclidiensEspaces euclidiens, produit scalaire
Énoncé du sujet
- Rappeler l'inégalité de Cauchy-Schwarz, en précisant le cas d'égalité.
- Soit un entier non nul
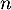 et des réels strictement positifs
et des réels strictement positifs
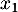 ,
, 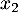 , … ,
, … , 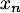 tels que
tels que
 .
.
Montrer que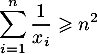 .
Préciser le cas d'égalité.
.
Préciser le cas d'égalité.
Correction
Correction
- Dans un espace euclidien
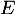 , l'inégalité de Cauchy-Schwarz s'écrit
, l'inégalité de Cauchy-Schwarz s'écrit
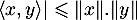 ,
avec égalité si et seulement si
,
avec égalité si et seulement si 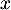 et
et 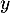 sont colinéaires.
sont colinéaires.
Dans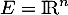 avec le produit scalaire canonique,
cette inégalité s'écrit, pour
avec le produit scalaire canonique,
cette inégalité s'écrit, pour
 et
et
 ,
,
![\[\left|\sum_{i=1}^nx_iy_i\right|\leqslant
\sqrt{\sum_{i=1}^nx_i^2}
\sqrt{\sum_{i=1}^ny_i^2}\]](/Generateur-Devoirs/Colles/EspaceEuclidien/CS1_c/8.png)
- On cherche, naturellement après la question précédente,
à utiliser des vecteurs
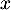 et
et 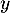 judicieux.
Pour pouvoir faire apparître les sommes
judicieux.
Pour pouvoir faire apparître les sommes
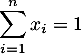 et
et
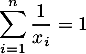 ,
on a tout intérêt à choisir
,
on a tout intérêt à choisir
![\[x=\lp\sqrt{x_1},\sqrt{x_2},\dots,\sqrt{x_n}\rp\]](/Generateur-Devoirs/Colles/EspaceEuclidien/CS1_c/13.png)
et
![\[y=\lp\dfrac1{\sqrt{x_1}}, \dfrac1{\sqrt{x_2}}, \dots , \dfrac1{\sqrt{x_n}}\rp\]](/Generateur-Devoirs/Colles/EspaceEuclidien/CS1_c/14.png)
On obtient alors, en écrivant l'inégalité de Cauchy-Schwarz:
![\[\left|\sum_{i=1}^n\sqrt{x_i}\dfrac1{\sqrt{x_i}}\right|\leqslant
\sqrt{\sum_{i=1}^nx_i} \sqrt{\sum_{i=1}^n\dfrac1{x_i}}\]](/Generateur-Devoirs/Colles/EspaceEuclidien/CS1_c/15.png)
![\[n=\left|\sum_{i=1}^n1\right|\leqslant
1\tm\sqrt{\sum_{i=1}^n\dfrac1{x_i}}\]](/Generateur-Devoirs/Colles/EspaceEuclidien/CS1_c/16.png)
d'où, en élevant au carré
![\[\sum_{i=1}^n\dfrac1{x_i}\geqslant n^2\]](/Generateur-Devoirs/Colles/EspaceEuclidien/CS1_c/17.png)
Il y a égalité si et seulement les vecteurs sont colinéaires, soit, s'il existe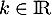 tel que
tel que
![\[\begin{array}{ll}x=ky
&\iff \forall1\leqslant i\leqslant n, \sqrt{x_i}=\dfrac{k}{\sqrt{x_i}}\\
&\iff \forall1\leqslant i\leqslant n, x_i=k\enar\]](/Generateur-Devoirs/Colles/EspaceEuclidien/CS1_c/19.png)
Ainsi toutes les coordonnées sont égales à la même constante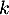 .
De plus,
.
De plus,
![\[1=\sum_{i=1}^nx_i=\sum_{i=1}^nk=nk \implies k=\dfrac1n\]](/Generateur-Devoirs/Colles/EspaceEuclidien/CS1_c/21.png)
d'où l'égalité si et seulement
![\[x_1=x_2=\dots=\dfrac1n\]](/Generateur-Devoirs/Colles/EspaceEuclidien/CS1_c/22.png)
Tag:Espaces euclidiens
Autres sujets au hasard:

Voir aussi: