Calculer l'intégrale …


Colle de mathématiques

Sujet de colle de maths:

Énoncé du sujet

Pour 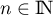$n\in\N$, calculer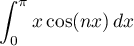 $\dsp\int_0^\pi x\cos(nx)\,dx$


Correction

Correction

Pour $n=0$, on a

\[\begin{array}{ll} \dsp\int_0^\pi x\cos(nx)\,dx &=\dsp\int_0^\pi x\,dx\\[1em] &=\lb\dfrac{x^2}2\rb_0^\pi =\dfrac{\pi^2}2 \enar\]


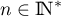Pour $n\in\N^*$, on intègre par parties:
\[\begin{array}{ll} \dsp\int_0^\pi x\cos(nx)\,dx &=\left[ x\dfrac{\sin(nx)}n\rb_0^\pi -\dsp\int_0^\pi\dfrac{\sin(nx)}n\,dx\\[1.2em] &=0-\dfrac1n\lb-\dfrac{\cos(nx)}n\rb_0^\pi\\[1em] &=\dfrac1{n^2}\lp\cos(n\pi)-1\right) =\dfrac1{n^2}\lp(-1)^n-1\right) \enar\]



Tag:Intégrale

Autres sujets au hasard: Lancer de dés

Voir aussi:
LongPage: h2: 3 - h3: 0