Base de l'image et du noyau d'une application linéaire
Colle de mathématiques
Sujet de colle de maths:- Applications linéairesApplications linéaires
Énoncé du sujet
On considère l'application linéaire 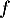 de
de 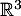 dans
dans 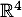 définie par
définie par
![\[f(x,y,z)=(x+z,y-x,z+y,x+y+2z)\]](/Generateur-Devoirs/Colles/Applin/exALbaseIm/4.png)
- Déterminer une base de
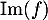 .
.
- Déterminer une base de
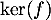 .
.
- L'application
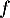 est-elle injective? surjective?
est-elle injective? surjective?
Correction
Correction
- On sait que
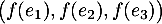 est une famille génératrice de
est une famille génératrice de 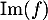 .
.
En utilisant la définition de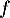 , on a :
, on a :
![\[\begin{array}{lcl}
f(e_1)&=&(1,-1,0,1)\\
f(e_2)&=&(0,1,1,1)\\
f(e_3)&=&(1,0,1,2)\\
\enar\]](/Generateur-Devoirs/Colles/Applin/exALbaseIm_c/4.png)
On peut alors chercher à savoir si cette famille est libre ou non.
On peut alors remarquer que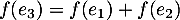 c'est-à-dire que
c'est-à-dire que  est combinaison linéaire de
est combinaison linéaire de 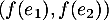 .
.
Ainsi, la famille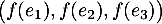 est liée, et la famille des deux vecteurs
est liée, et la famille des deux vecteurs 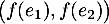 est même déjà génératrice de
est même déjà génératrice de  .
.
Cette famille de deux vecteurs est de plus libre car ces deux vecteurs sont non-nuls et ne sont pas colinéaires. On en déduit que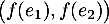 est une base de
est une base de 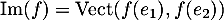 .
.
- On a :
![\[\begin{array}{ll}
&(x,y,z)\in\ker(f)\\[.5em]\iff& f(x,y,z)=(0,0,0,0)\\[.6em]
\iff&\left\{}\newcommand{\ra}{\right\}
\begin{array}{rcl}
x+z&=&0\\
-x+y&=&0\\
y+z&=&0\\
x+y+2z&=&0\\
\enar\right.\\[2.5em]
\iff&\left\{}\newcommand{\ra}{\right\}
\begin{array}{rcl}
x+z&=&0\\
y+z&=&0\\
y+z&=&0\\
y+z&=&0\\
\enar\right.\\[2.5em]
\iff&\left\{}\newcommand{\ra}{\right\}
\begin{array}{rcl}
x&=&-z\\
y&=&-z\\
z&=&z
\enar\right.\enar\]](/Generateur-Devoirs/Colles/Applin/exALbaseIm_c/13.png)
On en déduit que le vecteur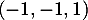 engendre
engendre 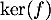 .
Comme il est non-nul, c'est une base de
.
Comme il est non-nul, c'est une base de 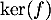 (qui est donc de dimension 1, ce que l'on peut aussi obtenir en utilisant le théorème du rang)
(qui est donc de dimension 1, ce que l'on peut aussi obtenir en utilisant le théorème du rang)
-
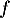 n'est pas injective, car son noyau n'est pas réduit au vecteur nul.
n'est pas injective, car son noyau n'est pas réduit au vecteur nul.
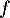 n'est pas surjective, car
n'est pas surjective, car
![\[\text{rg}(f)=\text{dim(Im(f)}=2\not=\text{dim}\lp\R^4\rp=4\]](/Generateur-Devoirs/Colles/Applin/exALbaseIm_c/19.png)
ce qui montre que l'image de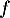 n'est pas
n'est pas 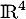 tout entier.
tout entier.
Tag:Applications linéaires
Autres sujets au hasard:

Voir aussi: