Application linéaire avec des polynômes de degré 2
Colle de mathématiques
Sujet de colle de maths:- Applications linéairesApplications linéaires
Énoncé du sujet
Montrer que ![$f:\la\begin{array}{ll}\R_2[X]\to \R_2[X] \\[.4em] P\mapsto P-XP'\enar\right.$](/Generateur-Devoirs/Colles/Applin/exALR2X/1.png) est une application linéaire.
est une application linéaire.
Déterminer son noyau et son image.
![$f:\la\begin{array}{ll}\R_2[X]\to \R_2[X] \\[.4em] P\mapsto P-XP'\enar\right.$](/Generateur-Devoirs/Colles/Applin/exALR2X/1.png) est une application linéaire.
est une application linéaire.
Déterminer son noyau et son image.
Correction
![$P,Q\in\R[X]$](/Generateur-Devoirs/Colles/Applin/exALR2X_c/1.png) et
et 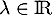 .
Alors
.
Alors
![\[\begin{array}{rcl}
f(\lambda P+Q)&=&(\lambda P+Q)-X(\lambda P+Q)'\\
&=&\lambda P+Q-X(\lambda P'+Q')\\
&=&\lambda (P-XP')+Q-XQ'\\
&=&\lambda f(P)+ f(Q).
\enar\]](/Generateur-Devoirs/Colles/Applin/exALR2X_c/3.png)
Ainsi,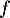 est bien une application linéaire.
est bien une application linéaire.
On s'intéresse au noyau de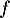 , donc aux polynômes
, donc aux polynômes ![$P\in\R_2[X]$](/Generateur-Devoirs/Colles/Applin/exALR2X_c/6.png) tels que
tels que
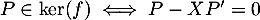 .
.
Soit donc![$P\in\R_2[X]\iff P(X)=aX^2+bX+c$](/Generateur-Devoirs/Colles/Applin/exALR2X_c/8.png) , alors
, alors
![\[f(P)=P-XP'\]](/Generateur-Devoirs/Colles/Applin/exALR2X_c/9.png)
c'est-à-dire
![\[\begin{array}{ll}f(P)(X)&=aX^2+bX+c-X\lp2aX+b\rp\\&=-aX^2+c\enar\]](/Generateur-Devoirs/Colles/Applin/exALR2X_c/10.png)
et ainsi,
![\[f(P)=0\iff a=c=0\]](/Generateur-Devoirs/Colles/Applin/exALR2X_c/11.png)
Les polynômes du noyau de sont donc de la forme
sont donc de la forme 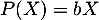 .
En notant le polynôme
.
En notant le polynôme 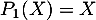 , on a donc
, on a donc
 .
.
On cherche maintenant l'image de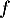 . D'après le théorème du rang,
. D'après le théorème du rang,
![\[\text{rg}(f)+\text{Im(Ker}(f)) = \text{dim}\lp\R_2[X]\rp=3\]](/Generateur-Devoirs/Colles/Applin/exALR2X_c/17.png)
et donc le rang de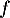 vaut 2.
vaut 2.
En notant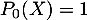 ,
, 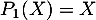 et
et 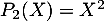 la base canonique de
la base canonique de ![$\R_2[X]$](/Generateur-Devoirs/Colles/Applin/exALR2X_c/22.png) ,
on sait que la famille
,
on sait que la famille 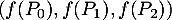 est génératrice de l'image de
est génératrice de l'image de 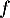 , et qu'elle est forcément liée puisque cette image est de dimension 2.
, et qu'elle est forcément liée puisque cette image est de dimension 2.
En effet on sait ici que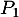 est dans le noyau de
est dans le noyau de 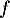 ...
...
Il suffit donc d'extraire une famille libre de deux éléments,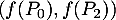 , avec
, avec
![\[f(P_0)(X)=P_0-XP_0'=1-X\tm0=1=P_0\]](/Generateur-Devoirs/Colles/Applin/exALR2X_c/28.png)
et
![\[f(P_2)(X)=P_2-XP_2'=x^2-X(2X)=-X^2=-P_2\]](/Generateur-Devoirs/Colles/Applin/exALR2X_c/29.png)
Ainsi,
![\[\text{Im}(f)=\text{Vect}\left( P_0,P_2\rp\]](/Generateur-Devoirs/Colles/Applin/exALR2X_c/30.png)
Correction
Soit![\[\begin{array}{rcl}
f(\lambda P+Q)&=&(\lambda P+Q)-X(\lambda P+Q)'\\
&=&\lambda P+Q-X(\lambda P'+Q')\\
&=&\lambda (P-XP')+Q-XQ'\\
&=&\lambda f(P)+ f(Q).
\enar\]](/Generateur-Devoirs/Colles/Applin/exALR2X_c/3.png)
Ainsi,
On s'intéresse au noyau de
Soit donc
c'est-à-dire
et ainsi,
Les polynômes du noyau de
On cherche maintenant l'image de
et donc le rang de
En notant
En effet on sait ici que
Il suffit donc d'extraire une famille libre de deux éléments,
et
Ainsi,
Tag:Applications linéaires
Autres sujets au hasard:

Voir aussi: