Application linéaire ? Noyau et image ?
Colle de mathématiques
Sujet de colle de maths:- Applications linéairesApplications linéaires
Énoncé du sujet
L'application
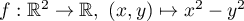 ;
est-elle linéaire ?
;
est-elle linéaire ?
Préciser son noyau et son image. Est-elle injective ? surjective ? bijective ?
Préciser son noyau et son image. Est-elle injective ? surjective ? bijective ?
Correction
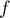 n'est clairement pas linéaire, à cause des carrés:
par exemple,
n'est clairement pas linéaire, à cause des carrés:
par exemple, 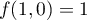 et
et 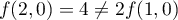 .
.
Ceci ne l'empêche pas de pouvoir être éventuellement injective, surjective, bijective.
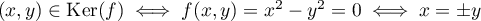 .
.
Ainsi, le noyau de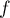 est composé des deux droites vectorielles
est composé des deux droites vectorielles
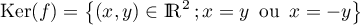 .
.
Pour l'injectivité, comme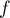 n'est pas linéaire, il faut revenir à la définition.
Ici
n'est pas linéaire, il faut revenir à la définition.
Ici 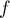 n'est clairement pas injective car, par exemple,
n'est clairement pas injective car, par exemple,
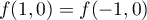 .
.
L'image de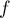 est
est 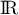 tout entier:
tout entier: 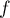 est surjective.
En effet, si
est surjective.
En effet, si 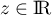 , alors,
si
, alors,
si 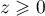 ,
, 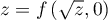 ,
tandis que si
,
tandis que si 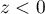 ,
, 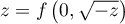 .
.
Comme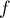 n'est pas injective, elle n'est pas non plus bijective.
n'est pas injective, elle n'est pas non plus bijective.
Correction
Ceci ne l'empêche pas de pouvoir être éventuellement injective, surjective, bijective.
Ainsi, le noyau de
Pour l'injectivité, comme
L'image de
Comme
Tag:Applications linéaires
Autres sujets au hasard:
