Suites numériques en Python

Première générale, spécialité maths

Suites définies explicitement, à partir d'une fonction: u_n = f (n)

Exercice 1:

Qu'affiche le programme suivant ?

def u(n):
    return 3*n-2

print(u(2))

n=10
print(u(n))

Modifier le programme précédent pour qu'il calcule les termes de la suite (u_n) définie par l'expression
u_n = 2n²−1 / n²+2
Afficher en particulier les termes u₁₀, u₁₀₀, et u₁₀₀₀.
Qu'observe-t-on pour des valeurs de plus en plus grandes de n ?

Exercice 2:

Afficher la suite des nombres.

Qu'affiche le programme suivant ?
```
def u(n):
    return n**2-3

for n in range(10):
    print(n,u(n))
```
(Voir le paragraphe boucles sur des entiers du chapitre sur les boucles for)
De la même façon, le programme suivant trace aussi les points correspondants sur un graphique
```
from pylab import *
def u(n):
    return n**2-3

for n in range(10):
    plot(n,u(n),'*b')

show()
```
(Voir éventuellement le paragraphe graphiques avec Python)
Modifier le programme précédent pour qu'il affiche et trace les 100 premiers termes de la suite (u_n) définie à la question 2. de l'exercice précédent.
Vers quelle valeur semble tendre les valeurs des termes de la suite lorsqu'on augmente n (et tend vers l'infini) ?

Calcul de seuil

Exercice 3:

Afficher la suite des nombres, jusqu'à un certain point

On considère la suite (u_n) définie explicitement par u_n = n² − n + 1
Calculer le rang n₀ à partir duquel on a, pour tout n ≥ n₀, u_n≥1000

Qu'affiche le programme suivant ?

def u(n):
    return n**2-n+1

n=0
while u(n)<1000:
    print(u(n))	     
    n=n+1

print(n)

(Voir aussi les boucles conditonnelles while)

On reprend la suite (u_n) définie à la question 2. de l'exercice 1. :
u_n = 2n²−1 / n²+2

On a vu que cette suite tend vers 2. Déterminer le rang n, à partir duquel u_n devient supérieur à 1,999 ?

Suites définies par récurrence: u_n+1 = f (u_n)

Exercice 4:

Qu'affiche le programme suivant ?
```
def u(n):
    if n==0:
        return 2
    else: 
        return 3*u(n-1)-2

print(u(0))
print(u(1))
print(u(2))

n=10
print(u(n))
```
La fonction définie et utilisée ici s'appelle une fonctions récursive: c'est une fonction qui s'appelle elle-même…
Modifier le programme précédent pour qu'il calcule les termes de la suite (u_n) définie par u₀ = 1 puis par l'expression
u_n+1 = 2u_n²+1 / u_n²+1
Afficher en particulier les premiers termes jusqu'à u₁₀, puis jusqu'à u₃₀.
Une autre manière de programmer les calculs des termes d'une suite récurrente est:
```
u=1
n=10
for i in range(n):
    u=(2*u**2+1)/(u**2+1)
    print(u)
```
qui calcule et affiche ici tous les premiers termes jusqu'à u₁₀.
1. Utiliser ce programme pour afficher en particulier les termes u₁₀, puis u₁₀₀ et u₁₀₀₀.
2. Comparer l'exécution à celle du programme précédent.
3. Qu'observe-t-on pour des valeurs de plus en plus grandes de n ?
On définit la fonction f telle que u_n+1 = f (u_n).
1. Étudier le sens de variation de f.
  (voir le paragraphe courbe représentative d'une fonction pour tracer la courbe de cette fonction avec Python)
2. Montrer que la suite (u_n) est croissante.
3. Montrer que la suite (u_n) est majorée par 2.
4. En déduire que la suite converge et donner une valeur approchée de sa limite.

Exercice 5:

On considère la suite (a_n) définie par a₁ = 0,5 puis par la relation de récurrence a_n+1 = 0,5a_n + 0,3.

Conjecturer, à l'aide Python, le sens de variation et la limite de cette suite.
Montrer que, pour tout entier n ≥ 1, on a 0 ≤ u_n ≤ 0,6.
Démontrer les conjectures précédentes: la suite (a_n) est croissante et convergente, et calculer exactement sa limite.

Somme des termes d'une suite

Exercice 6:

Que calcule le programme suivant:

n=int(input("Entrer n: "))
s=0
for i in range(n+1):
    s=s+i
    print("i= ",i, " - s= ",s)

Modifier le programme précédent pour qu'il calcule, à un nombre n donné (ou demandé à l'utilisateur), les sommes:
- S = 1 + 1/2 + 1/3 + 1/4 + 1/5 + …
- T = 1 + 1/2² + 1/3² + 1/4² + 1/5² + …
- U = 1 + 1/2¹ + 1/2² + 1/2³ + 1/2⁴ + …
Quelles conjectures peut-on faire pour ces trois suites ?

Exercice 7:

On considère la suite (u_n) définie par u₀ = 1 et par la relation de récurrence: pour tout entier naturel n , u_n+1 = f (u_n), où la fonction f est définie sur l'intervalle [ 0 ; +∞ [ par

f (x) = 5 − 4/x + 2

On définit de plus, pour tout entier naturel n, la somme (S_n) par

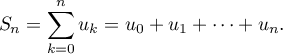
$S_n = \sum_{k=0}^{n} u_k = u_0 + u_1 + \cdots + u_n.$

Calculer S₀, S₁ et S₂. Donner une valeur approchée des résultats à 10⁻² près.
Compléter le programme Python suivant pour qu'il affiche la somme S_n pour la valeur de l'entier n demandée à l'utilisateur.
```
u=1
s=u
i=0
n=int(input("Entrer un nombre:"))

while … 
    i=i+1
    u= … 
    s= … 

print …
```
Faire l'exercice complet (exercice posé au Bac S, en Nouvelle Calédonie en 2014).

Exercice 8:

Une association sportive compte 500 adhérents. On constate que, chaque mois,

5% des adhérents ne renouvellent pas leur adhésion
30 nouveaux adhérents s'inscrivent dans l'association

L'adhésion mensuelle coûte 10 euros.

Écrire un programme qui calcule et affiche le nombre d'adhérents dans l'association mois après mois, pendant 2 ans.
Calculer le montant total des cotisations perçues en 2 ans.
Quel devrait être le montant de l'adhésion mensuelle pour que l'association puisse financer complètement une nouvelle installation qui coûte 20 000 euros ?

Un exemple de problème: dynamique de populations

Exercice 9:

Un village comptait 2000 habitants l'année 2000. Chaque année depuis, cette population augmente de 3% d'une année à la suivante.
1. Écrire un programme qui calcule le nombre d'habitants dans ce village en 2001, puis 2002, puis 2010, puis cette année.
2. Modifier le programme précédent pour qu'il détermine en quelle année la population du village aura triplé.
On observe maintenant des flux de population entre deux villes A et B. Il y a maintenant 50000 personnes qui habitent dans la ville A et 2000 dans le village B.
Chaque année, 10% de la population de la ville A déménage pour aller habiter dans le village B, tandis que 30% des habitants du village B viennent habiter dans la ville A.
Comment vont évoluer les populations de ces deux villes ?
1. Écrire un programme qui calcule le nombre d'habitants, année aprés année, dans la ville A et dans le village B. Représenter graphiquement, sur un même graphique, l'évolution de ces populations en fontion de l'année, en rouge pour la ville A et bleu pour B.
2. La population de la ville A évolue comme précédemment: 10% des habitants vont chaque année habiter en B. 30% des habitants de B vont encore aussi chaque année se déplacer vers A.
  On considère maintenant de plus que, chaque année, 5% des habitants de B vont ailleurs, ni en A ni en B.
  Modifier le programme précédent pour rendre compte graphiquement de la nouvelle évolution des populations.