Loi géométrique tronquée: service de dépannage téléphonique

Exercice corrigé - Spécialité maths, première générale

Un client cherche à joindre par téléphone un service de dépannage. La probabilité que son appel soit pris sans attente est de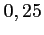

. Si son appel n'est pas pris sans attente, le client raccroche son téléphone et fait une autre tentative.

Le client fait au maximum trois tentatives.

On note la variable aléatoire égale au rang de son premier appel aboutissant sans attente. Si au bout de trois appels le client n'a pas réussi à joindre le service de dépannage sans attente, on convient alors que .

On note l'événement: "Le client est mis en relation avec le service de dépannage sans attente."

Représenter la situation par un arbre de probabilités.
Quelles valeurs peut prendre la variable aléatoire ?
Déterminer alors la loi de probabiltié de (présenter les résultats dans un tableau).
Déterminer l'espérance de la variable aléatoire , et interpréter ce résultat.

Correction

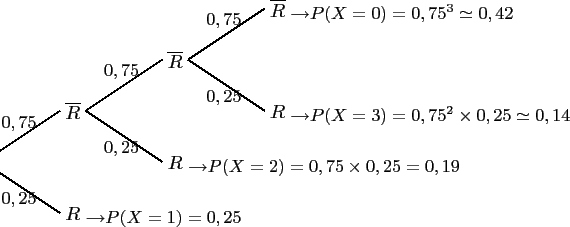
$\begin{pspicture}(-0.5,-1.4)(6,2.5) \psline(0,0)(1.5,1)\rput(1.75,1){$\overline... ...2$} \rput(4.7,2.75){\small$0,75$}\rput(4.7,1.25){\small$0,25$} \end{pspicture}$
La variable aléatoire 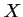peut être égale à: 0 ; 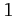; 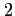ou .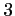

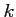
0 1 2 3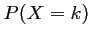

0,42 0,25 0,19 0,14
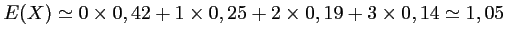$E(X)\simeq0\times 0,42+1\times 0,25+2\times 0,19+3\times 0,14 \simeq1,05$ :
en moyenne, le client joindra le service clientèle en un peu plus d'un appel.

Cacher la correction

Tag:Probabilités conditionnelles

Autres sujets au hasard:

Voir aussi:

	0	1	2	3
	0,42	0,25	0,19	0,14