Equation de la médiatrice, intersection de droites et équation de cercle
Exercice corrigé - Spécialité maths, première générale
Dans le plan est rapporté à un repère orthonormal
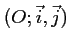 , on considère les points
, on considère les points
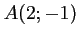 et
et 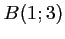 , et la droite
, et la droite
 d'équation
d'équation  .
.
- Déterminer l'équation de la médiatrice
 de
de ![$ [AB]$](/Generateur-Devoirs/1S/Chap6/ex2_img7.png) .
.
- Représenter sur une figure les droites
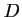 et
et  .
.
- Calculer les coordonnées du point
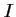 , intersection des droites
, intersection des droites
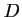 et
et  .
.
- Déterminer le rayon du cercle
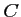 passant par
passant par 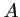 et
et 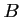 et dont
le centre est sur la droite
et dont
le centre est sur la droite 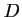 .
.
- Déterminer l'équation du cercle
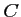 .
.
Correction
Cacher la correction
- Soit
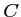 le milieu de
le milieu de ![$ [AB]$](/Generateur-Devoirs/1S/Chap6/ex2_c_img2.png) , alors
, alors 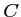 a pour coordonnées
a pour coordonnées
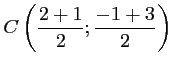 ,
soit
,
soit
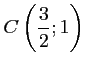 .
.
De plus,
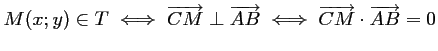 .
.
On a les coordonnées des vecteurs:
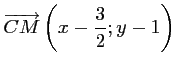 et
et
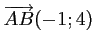 ,
d'où,
,
d'où,
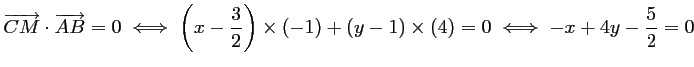
La médiatrice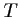 a donc pour équation:
a donc pour équation:
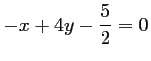 .
.
-
![\begin{pspicture}(-4,-4)(4,3.5)
\psline[arrowsize=5pt]{->}(-3.5,0)(3.5,0)
\psl...
... \rput(1,3){$\times $}\rput(1.2,3.2){$B$}
\rput(-1.2,0.6){$I$}
\end{pspicture}](/Generateur-Devoirs/1S/Chap6/ex2_c_img11.png)
- Soit
 ,
alors,
,
alors,
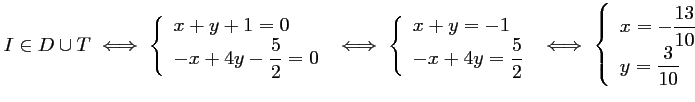
Ainsi, les coordonnées de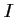 sont
sont
 .
.
- Le centre du cercle passant par
 et
et  est sur la médiatrice
est sur la médiatrice
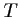 de
de ![$ [AB]$](/Generateur-Devoirs/1S/Chap6/ex2_c_img2.png) .
Comme ce centre doit aussi être sur la droite
.
Comme ce centre doit aussi être sur la droite 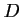 , on en déduit
qu'il s'agit du point
, on en déduit
qu'il s'agit du point 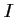 .
.
Le rayon du cercle est alors
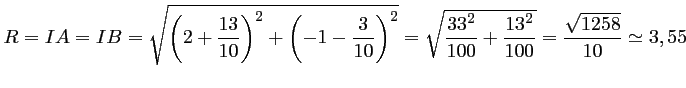
- Le cercle
 a pour équation:
a pour équation:
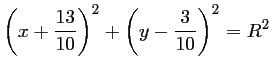
Cacher la correction
Tag:Produit scalaire
Voir aussi:
