Efficacité de stages de révision dans une université

Exercice corrigé - Spécialité maths, première générale

Des étudiants sont inscrits en L1 dans une université. À l'approche des examens, un stage de révision est organisé. L'expérience montre que 3/4 des étudiants ayant suivi le stage de révision réussissent leurs examens et 1/3 des étudiants n'ayant pas suivi le stage ne réussissent pas leurs examens. On sait de plus que 20% des étudiants de L1 suivent le stage de révision.
On choisit un étudiant au hasard et on considère les évènements : A : « l'étudiant a suivi le stage de révision»  et B : « l'étudiant a réussi ses examens».
  1. Construire un arbre de probabilité traduisant la situation étudiée.
  2. Si l'étudiant choisi a suivi le stage, quelle est la probabilité qu'il n'ait pas réussi ses examens ?
  3. Quelle est la probabilité que l'étudiant choisi ait suivi le stage et réussi ses examens ?
  4. Quelle est la probabilité que l'étudiant choisi ait réussi ses examens ?
  5. Sachant que l'étudiant choisi a réussi ses examens, quelle est la probabilité qu'il ait suivi le stage ?
  6. (Bonus) L'université trouve que les résultats aux examens de L1 sont trop faibles et aimerait inciter plus d'étudiants à s'inscrire au stage de révision afin qu'au moins 70% des étudiants de L1 réussissent leurs examens. Sachant qu’il y a 300 étudiants inscrits en L1, combien de places faudra-t-il prévoir au minimum lors du stage pour espérer atteindre cet objectif ?

Correction

  1. \[\psset{xunit=1cm,yunit=.6cm} \begin{pspicture}(-2,-3)(5,2.6) \psline(0,0)(1.5,1.5)\rput(1.75,1.5){$A$}\rput(.7,1.3){$20\%$} \psline(2,1.5)(3.5,2.25)\rput(3.75,2.25){$B$}\rput(2.7,2.3){$3/4$} \psline(2,1.5)(3.5,0.75)\rput(3.75,0.75){$\overline{B}$}\rput(2.7,.6){$1/4$} \psline(0,0)(1.5,-1.5)\rput(1.75,-1.5){$\overline{A}$}\rput(.7,-1.3){$80\%$} \psline(2,-1.5)(3.5,-0.75)\rput(3.75,-0.75){$B$}\rput(2.7,-.6){$2/3$} \psline(2,-1.5)(3.5,-2.25)\rput(3.75,-2.25){$\overline{B}$}\rput(2.7,-2.4){$1/3$} \end{pspicture}\]

  2. Sachant que l'étudiant choisi a suivi le stage, la probabilité qu'il n'ait pas réussi ses examens est déjà inscrite dans l'arbre
    \[P_A(\overline{B})=\dfrac14\]

  3. La probabilité que l'étudiant choisi ait suivi le stage et réussi ses examens est
    \[P(A\cap B)=20\%\tm\dfrac34=15\%\]

  4. La probabilité que l'étudiant choisi ait réussi ses examens est, d'après la formule des probabilités totales,
    \[P(B)=20\%\tm\dfrac34+80\%\tm\dfrac23\simeq0,68\]

  5. Sachant que l'étudiant choisi a réussi ses examens, la probabilité qu'il ait suivi le stage est
    \[P_B(A)=\dfrac{P(A\cap B)}{P(B)}\simeq\dfrac{15\%}{68\%}\simeq0,22=22\%\]

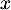  6. On note $x$ le nombre de places au stage, et on a alors l'arbre
    \[\psset{xunit=1cm,yunit=.6cm} \begin{pspicture}(-2,-3)(5,2.6) \psline(0,0)(1.5,1.5)\rput(1.75,1.5){$A$}\rput(.7,1.3){$\frac{x}{300}$} \psline(2,1.5)(3.5,2.25)\rput(3.75,2.25){$B$}\rput(2.7,2.3){$3/4$} \psline(2,1.5)(3.5,0.75)\rput(3.75,0.75){$\overline{B}$}\rput(2.7,.6){$1/4$} \psline(0,0)(1.5,-1.5)\rput(1.75,-1.5){$\overline{A}$}\rput(.4,-1.3){$1-\frac{x}{300}$} \psline(2,-1.5)(3.5,-0.75)\rput(3.75,-0.75){$B$}\rput(2.7,-.6){$2/3$} \psline(2,-1.5)(3.5,-2.25)\rput(3.75,-2.25){$\overline{B}$}\rput(2.7,-2.4){$1/3$} \end{pspicture}\]

    On veut maintenant que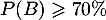 $P(B)\geqslant70\%$, avec
    \[P(B)=\dfrac{x}{300}\tm\dfrac34+\lp1-\dfrac{x}{300}\rp\dfrac23 =\dfrac1{12}\tm\dfrac{x}{300}+\dfrac23\]

    et donc
    \[P(B)\geqslant70\% \iff\dfrac1{12}\tm\dfrac{x}{300}+\dfrac23\geqslant70\% \iff x\geqslant300\tm12\lp70\%-\dfrac23\rp=120 \]

    Il faudra donc pévoir 120 places pour arriver à ce taux de réussite.


Cacher la correction


Tag:Probabilités conditionnelles

Autres sujets au hasard: Lancer de dés


Voir aussi:
LongPage: h2: 1 - h3: 0