Diverses équations et inéquations utilisant du 2nd degré (2)
Exercice corrigé - Spécialité maths, première générale
Résoudre sur  les équations ou inéquations:
les équations ou inéquations:
a)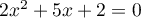
b)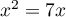
c)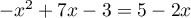
d)
e)
f)
a)
b)
c)
d)
e)
f)
Correction
a)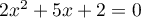 est un trinôme du 2nd degré de discriminant
est un trinôme du 2nd degré de discriminant
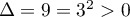 et admet donc deux racines réelles:
et admet donc deux racines réelles:
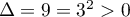
b)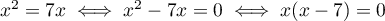 soit
soit  ou
ou 
c)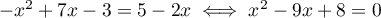
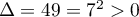 ,
donc l'équation admet deux racines réelles distinctes :
,
donc l'équation admet deux racines réelles distinctes :
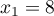 et
et 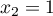 .
.
d) C'est le trinôme du a) qui a deux racines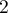 et
et 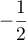 .
Ce trinôme est donc strictement négatif sur
.
Ce trinôme est donc strictement négatif sur
![$\mathcal{S}=\Bigl]-2;-\dfrac12\Bigr[$](/Generateur-Devoirs/1S/Chap1/ex1.2_c/13.png) .
.
e) On cherche le signe du trinôme du dénominateur.
Son discriminant est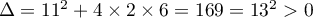 .
.
Le trinôme admet donc deux racines réelles distinctes: et
et 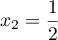 .
.
On peut alors dresser le tableau de signe de cette fraction:
![\[\begin{tabular}{|c|lcccccccr|}\hline
$x$ & $-\infty$ & &$-6$& &$-\frac{2}{3}$& &$\frac{1}{2}$&&$+\infty$
\\\hline
$3x+2$& &-& $|$ &-& \mbox{$0\hspace{-0.67em}\mid$} &+&$|$&+&\\\hline
$2x^2+11x-6$& &+& \zb&-& $|$ &-&\zb&+&\\\hline
$\frac{3x+2}{2x^2+11x-6}$
&-& \db&+& \mbox{$0\hspace{-0.67em}\mid$} &-&\db&+& \\\hline
\end{tabular}
\]](/Generateur-Devoirs/1S/Chap1/ex1.2_c/17.png)
On en déduit les solutions de l'inéquation:![$\mathcal{S}=\bigr]-6\,;\,-\dfrac{2}{3}\bigr]
\cup\bigr]\dfrac{1}{2}\,;\,+\infty\bigl[$](/Generateur-Devoirs/1S/Chap1/ex1.2_c/18.png)
f)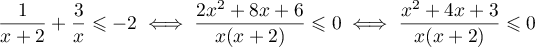
Le numérateur est un trinôme du second degré de discriminant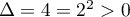 et admet donc deux racines réelles distinctes
et admet donc deux racines réelles distinctes
 et
et 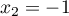 . On peut alors dresser le tableau de signes:
. On peut alors dresser le tableau de signes:
![\[\begin{tabular}{|c|lcccccccccr|}\hline
$x$ & $-\infty$ & &$-3$& &$-2$& &$-1$& &$0$& &$+\infty$
\\\hline
$x^2+4x+3$& &+& \zb&-& $|$ &-&\zb&+& $|$ &$+$&\\\hline
$x(x+2)$& &+& $|$ &+& \mbox{$0\hspace{-0.67em}\mid$} &-&$|$&-& \mbox{$0\hspace{-0.67em}\mid$} & +&\\\hline
$\dfrac{x^2+4x+3}{x(x+2)}$
& &+& \mbox{$0\hspace{-0.67em}\mid$} &-& \mbox{$\hspace{0.1em}|\hspace{-0.67em}\mid$} &+&\mbox{$0\hspace{-0.67em}\mid$}&-& \mbox{$\hspace{0.1em}|\hspace{-0.67em}\mid$} & +&\\\hline
\end{tabular}
\]](/Generateur-Devoirs/1S/Chap1/ex1.2_c/23.png)
Ainsi,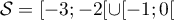 .
.
Cacher la correction
a)
b)
c)
d) C'est le trinôme du a) qui a deux racines
e) On cherche le signe du trinôme du dénominateur.
Son discriminant est
Le trinôme admet donc deux racines réelles distinctes:
On peut alors dresser le tableau de signe de cette fraction:
![\[\begin{tabular}{|c|lcccccccr|}\hline
$x$ & $-\infty$ & &$-6$& &$-\frac{2}{3}$& &$\frac{1}{2}$&&$+\infty$
\\\hline
$3x+2$& &-& $|$ &-& \mbox{$0\hspace{-0.67em}\mid$} &+&$|$&+&\\\hline
$2x^2+11x-6$& &+& \zb&-& $|$ &-&\zb&+&\\\hline
$\frac{3x+2}{2x^2+11x-6}$
&-& \db&+& \mbox{$0\hspace{-0.67em}\mid$} &-&\db&+& \\\hline
\end{tabular}
\]](/Generateur-Devoirs/1S/Chap1/ex1.2_c/17.png)
On en déduit les solutions de l'inéquation:
f)
Le numérateur est un trinôme du second degré de discriminant
![\[\begin{tabular}{|c|lcccccccccr|}\hline
$x$ & $-\infty$ & &$-3$& &$-2$& &$-1$& &$0$& &$+\infty$
\\\hline
$x^2+4x+3$& &+& \zb&-& $|$ &-&\zb&+& $|$ &$+$&\\\hline
$x(x+2)$& &+& $|$ &+& \mbox{$0\hspace{-0.67em}\mid$} &-&$|$&-& \mbox{$0\hspace{-0.67em}\mid$} & +&\\\hline
$\dfrac{x^2+4x+3}{x(x+2)}$
& &+& \mbox{$0\hspace{-0.67em}\mid$} &-& \mbox{$\hspace{0.1em}|\hspace{-0.67em}\mid$} &+&\mbox{$0\hspace{-0.67em}\mid$}&-& \mbox{$\hspace{0.1em}|\hspace{-0.67em}\mid$} & +&\\\hline
\end{tabular}
\]](/Generateur-Devoirs/1S/Chap1/ex1.2_c/23.png)
Ainsi,
Cacher la correction
Tag:2nd degré
Voir aussi:
