Produit multiple de 6
Exercice corrigé - Maths expertes, terminale générale
Énoncé
Soit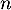 
un entier relatif. Montrer que l'entier 
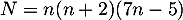est toujours un multiple de 6.
(on pourra utiliser un tableau de congruences).
un entier relatif. Montrer que l'entier est toujours un multiple de 6.(on pourra utiliser un tableau de congruences).
Correction
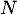selon celles de 
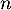modulo 6:
![\[ \renewcommand{\arraystretch}{1.6}
\begin{tabular}{|c|c|c|c|c|c|c|}\hline
$n\equiv \dots [6]$ & 0 & 1 & 2 & 3 & 4 & 5\\\hline
$n+2\equiv \dots [6]$ & 2 & 3 & 4 & 5 & 0 & 1\\\hline
$7n-5\equiv \dots [6]$ & 1 & 2 & 3 & 4 & 5 & 0\\\hline
$N\equiv\dots[6]$ & 0 & 0 & 0 & 0 & 0 & 0 \\\hline
\end{tabular}\]](/Generateur-Devoirs/Mex/EuclCong/expm6_c/3.png)
Ainsi, dans tous les cas on a![$N=n(n+2)(7n-5)\equiv0[6]$](/Generateur-Devoirs/Mex/EuclCong/expm6_c/4.png)
, ce qui signifie exactement que l'entier 
est un multiple de 6.
Correction
On construit le tableau des congruences de selon celles de modulo 6:
Ainsi, dans tous les cas on a
, ce qui signifie exactement que l'entier est un multiple de 6.
Tag:Division euclidienne - Congruences
Autres sujets au hasard:
Voir aussi: