Petit binôme de Newton pour un complexe

Exercice corrigé - Maths expertes, terminale générale

Énoncé

On considère le nombre complexe 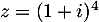$z=(1+i)^4$.
  1. En utilisant les coefficients du triangle de Pascal, développer et écrire sous forme algébrique le nombre complexe $z$.
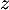  2. Écrire sous forme exponentielle le nombre complexe 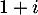$1+i$ et retrouver le résultat précédent.



Correction

Correction

  1. On écrit le triangle de Pascal jusqu'à la 4-ième ligne:
    \[\begin{tabular}{c|llllll}n&\\\hline1&1&1\\2&1&2&1\\3&1&3&3&1\\4&1&4&6&4&1\end{tabular}\]

    et alors le binôme de Newton s'écrit
    \[\begin{array}{ll}(1+i)^4&=1^4+4\tm1^3i^1+6\tm1^2i^2+4\tm1^1i^3+i^4\\ &=1+4i-6-4i+1\\ &=-4 \enar\]


  2. On calcule d'abord le module: 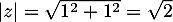$|z|=\sqrt{1^2+1^2}=\sqrt2$ et alors 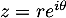$z=re^{i\theta}$ avec
    \[\la\begin{array}{ll}\cos\theta&=\dfrac1{\sqrt2}=\dfrac{\sqrt2}2\\ \sin\theta&=\dfrac1{\sqrt2}=\dfrac{\sqrt2}2\enar\right.\]

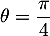    d'où $\theta=\dfrac\pi4$ et on trouve alors l'écriture exponentielle
    \[1+i=\sqrt2e^{i\frac\pi4}\]

    et donc,
    \[z=(1+i)^4=\lp\sqrt2e^{i\frac\pi4}\rp^4=\sqrt2^4e^{i\pi}\]

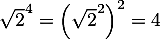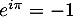    où $\sqrt2^4=\lp\sqrt2^2\rp^2=4$ et $e^{i\pi}=-1$.
    On retrouve bien ainsi le résultat de la question précédente, à savoir
    \[z=(1+i)^4=-4\]



Tag:Polynomes complexes

Autres sujets au hasard: Lancer de dés


Voir aussi:

Quelques devoirs


LongPage: h2: 3 - h3: 0
Énoncé