Divisibilité par 7, par récurrence
Exercice corrigé - Maths expertes, terminale générale
Énoncé
Montrer par récurrence que pour tout entier naturel 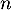 , le nombre
, le nombre 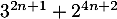 est divisible par 7.
est divisible par 7.
Correction
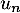 le nombre
le nombre
![\[u_n=3^{2n+1}+2^{4n+2}\]](/Generateur-Devoirs/Mex/EuclCong/exdrec7_c/2.png)
et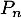 la propriété: «
la propriété: « 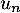 est divisible par 7»
est divisible par 7»
Initialisation: Pour , on a
, on a 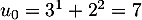 qui est bien divisible par 7.
qui est bien divisible par 7.
La propriété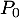 est donc bien vraie.
est donc bien vraie.
Hérédité: Supposons que pour un entier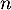 ,
, 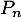 soit vraie, c'est-à-dire que
soit vraie, c'est-à-dire que 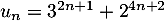 est divisible par 7.
est divisible par 7.
Alors, au rang suivant,
![\[\begin{array}{ll}u_{n+1}=3^{2(n+1)+1}+2^{4(n+1)+2}
=3^{2n+3}+2^{4n+6}\enar\]](/Generateur-Devoirs/Mex/EuclCong/exdrec7_c/11.png)
On cherche à faire intervenir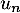 et donc on écrit
et donc on écrit
![\[u_{n+1}=3^{2n+1}\tm3^2+2^{4n+2}\tm2^4\]](/Generateur-Devoirs/Mex/EuclCong/exdrec7_c/13.png)
or on a![$3^2=9\equiv2\,[7]$](/Generateur-Devoirs/Mex/EuclCong/exdrec7_c/14.png) et
et ![$2^4=16\equiv2\,[7]$](/Generateur-Devoirs/Mex/EuclCong/exdrec7_c/15.png) , et donc
, et donc
![\[u_{n+1}\equiv3^{2n+1}\tm2+2^{4n+2}\tm2\,[7]\]](/Generateur-Devoirs/Mex/EuclCong/exdrec7_c/16.png)
et en factorisant par 2 on retrouve justement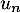 :
:
![\[u_{n+1}\equiv2u_n\,[7]\]](/Generateur-Devoirs/Mex/EuclCong/exdrec7_c/18.png)
Or, par hypothèse de récurrence on a supposé que![$u_n\equiv0\,[7]$](/Generateur-Devoirs/Mex/EuclCong/exdrec7_c/19.png) et donc on a aussi par conséquent
et donc on a aussi par conséquent
![\[u_{n+1}\equiv0\,[7]\]](/Generateur-Devoirs/Mex/EuclCong/exdrec7_c/20.png)
ce qui montre que la propriété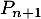 est encore vraie.
est encore vraie.
Conclusion: On vient de démontrer, d'après le principe de récurrence, que pour tout entier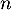 , le nombre
, le nombre 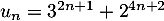 est divisible par 7.
est divisible par 7.
Correction
On démontre cette propriété par récurrence. On noteet
Initialisation: Pour
La propriété
Hérédité: Supposons que pour un entier
Alors, au rang suivant,
On cherche à faire intervenir
or on a
et en factorisant par 2 on retrouve justement
Or, par hypothèse de récurrence on a supposé que
ce qui montre que la propriété
Conclusion: On vient de démontrer, d'après le principe de récurrence, que pour tout entier
Tag:Division euclidienne - Congruences
Voir aussi:
Quelques devoirs
sur les nombres complexes: résolution d'équations et forme algébrique. Arithmétique, divisibilité et division euclidienne
sur les nombres complexes et polynômes. Résolution d'une éuqation complexe. Racine d'un polynôme et factorisation du polynôme. Quotients et restes de division euclidienne. Divisiblité par 8
d'arithmétique (division euclidienne et congruences) et factorisation des polynômes complexes.
sur le plan complexe, les nombres complexes en géométrie, et les congruences en arithmétiques. Ecritures algébriques, trigonométrique et exponentielle d'un nombre complexe. Application au calcul de la puissance d'un nombre complexe. Calcul des valeurs exactes des cosinus et sinus de π/12. Congruences et chiffre des unités d'une puissance
sur le plan complexe, les nombres complexes en géométrie, et les congruences en arithmétiques. Ecritures algébriques, trigonométrique et exponentielle d'un nombre complexe. Application au calcul de la puissance d'un nombre complexe. Critère de divisibilité par 19
