Oral du bac: intégration et géométrie
Exponentielle, intégrales, géométrie dans l'espace
- L'utilisation d'une calculatrice est autorisée.
- La qualité des raisonnements, de l'expression, et la précision des justifications prendront une part importante dans l'appréciation de l'interrogation orale.
- Il s'agit d'une épreuve orale: il n'est pas indispensable de rédiger l'ensemble des réponses, des calculs, du raisonnement …
Par contre vous devez être en mesure d'apporter toutes les justifications nécessaires.
L'exposé de la méthode et du raisonnement sera pris en compte.
Exercice 1: Fonction exponentielle, primitive, variations et intégrale
Soit 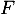 la fonction définie sur
la fonction définie sur 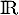 par l'expression:
par l'expression: 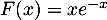 .
.
- Montrer que
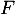 est une primitive de la fonction
est une primitive de la fonction 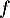 définie sur
définie sur
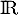 par
par 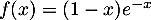 .
.
Existe-t'il d'autres primitives de la fonction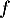 ?
?
- Dresser le tableau de variation de
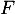 .
.
- Calculer
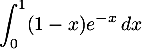 .
.
Correction exercice 1
Cacher la correction
-
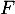 est une primitive de
est une primitive de 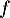 signifie que
signifie que 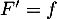 : il faut donc calculer la dérivée de
: il faut donc calculer la dérivée de 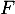 .
.
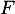 est un produit de deux fonctions:
est un produit de deux fonctions: 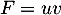 ,
avec
,
avec 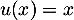 , donc
, donc 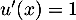 , et
, et 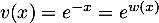 ,
donc
,
donc 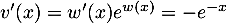 .
.
On a alors,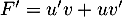 , soit
, soit
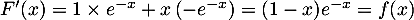 .
.
Ainsi,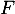 est bien une primitive de
est bien une primitive de 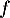 .
.
L'ensemble des primitives de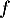 est donc l'ensemble des fonctions qui
s'écrivent sous la forme
est donc l'ensemble des fonctions qui
s'écrivent sous la forme 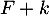 , où
, où 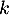 est un réel quelconque.
est un réel quelconque.
- Les variations de
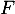 sont données par le signe de sa dérivée
sont données par le signe de sa dérivée 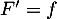 .
.
![\[\begin{tabular}{|c|ccccc|}\hline
$x$&$-\infty$&&1&&$+\infty$\\\hline
$1-x$&&$+$&\zb&$-$&\\\hline
$e^{-x}$&&$+$&$|$&$+$&\\\hline
$(1-x)e^{-x}$&&$+$&\zb&$-$&\\\hline
&&&$e^{-1}$&&\\
$F$&&\Large{$\nearrow$}&&\Large{$\searrow$}&\\
&$-\infty$&&&&$0$\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapIntegration/exOral04_c/20.png)
On peut compléter avec les limites:- en
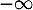 , il n'y a pas de problème particulier:
, il n'y a pas de problème particulier:
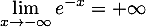 , et donc, par produit des limites,
, et donc, par produit des limites,
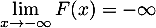
- en
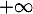 on est face à une forme indéterminée "
on est face à une forme indéterminée "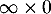 ".
".
Il s'agit en fait de la propriété de croissances comparées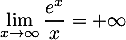 et donc
et donc
![\[\lim_{x\to+\infty}xe^{-x}=\lim_{x\to\infty}\dfrac{x}{e^x}
=\lim_{x\to\infty}\dfrac1{\frac{e^x}{x}}=0\]](/Generateur-Devoirs/TS/ChapIntegration/exOral04_c/27.png)
- en
- Comme
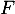 est une primitive de
est une primitive de 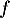 , on
, on
![\[\int_0^1 f(x)dx=F(1)-F(0)=1e^{-1}-0e^{-0}=\dfrac1e\]](/Generateur-Devoirs/TS/ChapIntegration/exOral04_c/30.png)
Cacher la correction
Exercice 2: Intersection et distance entre un plan (équation cartésienne) et une droite (représentée paramétriquement)
Dans l'espace muni du repère orthonormal 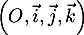 on considère le plan
on considère le plan 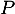 d'équation
d'équation
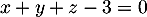 ainsi que le point
ainsi que le point 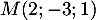 .
.
- Le point
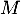 est-il dans le plan
est-il dans le plan 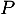 ?
?
- Donner une représentation paramétrique de la droite
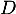 passant
par
passant
par 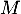 et orthogonale à
et orthogonale à 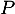 .
.
- Déterminer les coordonnées du point
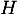 intersection de
intersection de 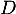 et
et 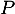 .
.
- En déduire la distance du point
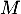 au plan
au plan 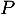 .
.
Correction exercice 2
Cacher la correction
-
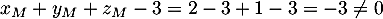 donc
donc 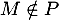 .
.
-
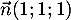 est un vecteur normal de
est un vecteur normal de 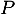 ,
la droite
,
la droite 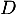 passant par
passant par 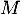 et orthogonale à
et orthogonale à 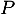 admet donc
comme représentatation paramétrique:
admet donc
comme représentatation paramétrique:
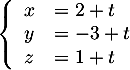
- Comme
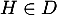 , il existe un réel
, il existe un réel 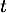 tel que
tel que 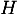 ait pour
coordonnées
ait pour
coordonnées
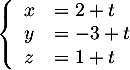 Comme de plus
Comme de plus 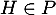 , ses coordonnées vérifient l'équation de
, ses coordonnées vérifient l'équation de 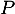 donc
donc 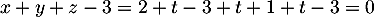 ,
soit
,
soit 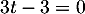 et donc
et donc 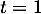 .
.
On a ainsi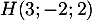 .
.
- La distance du point
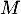 au plan
au plan 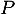 est
est 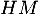 .
Comme
.
Comme 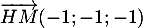 , on a donc
, on a donc 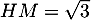 .
.
Cacher la correction
Voir aussi: