Une petite récurrence
Exercice corrigé - Spécialité maths, terminale générale
On considère la suite 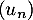 définie par:
définie par:
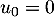 et, pour tout entier naturel,
et, pour tout entier naturel,
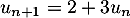 .
.
Démontrer que, pour tout entier naturel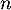 ,
,
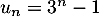 .
.
Démontrer que, pour tout entier naturel
Correction
On note, pour tout entier naturel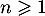 ,
, 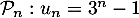 .
.
Initialisation: Pour , on a
, on a 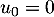 , et
, et
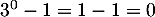 .
.
Ainsi, initialement au rang ,
, 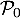 est vraie.
est vraie.
Hérédité: Supposons que pour un certain entier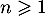 ,
, 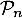 est vraie,
c'est-à-dire que
est vraie,
c'est-à-dire que 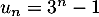 , alors,
, alors,
![\[\begin{array}{ll}
u_{n+1}&=2+3u_n\\
&=2+3\lp3^n-1\rp\\
&=2+3^{n+1}-3\\
&=3^{n+1}-1
\enar\]](/Generateur-Devoirs/TS/ChapSuites/exrec_c/11.png)
ce qui montre que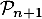 est encore vraie.
est encore vraie.
Conclusion: On a donc montré, d'après le principe de récurrence, que pour tout entier naturel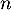 ,
,
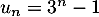 .
.
Cacher la correction
On note, pour tout entier naturel
Initialisation: Pour
Ainsi, initialement au rang
Hérédité: Supposons que pour un certain entier
![\[\begin{array}{ll}
u_{n+1}&=2+3u_n\\
&=2+3\lp3^n-1\rp\\
&=2+3^{n+1}-3\\
&=3^{n+1}-1
\enar\]](/Generateur-Devoirs/TS/ChapSuites/exrec_c/11.png)
ce qui montre que
Conclusion: On a donc montré, d'après le principe de récurrence, que pour tout entier naturel
Cacher la correction
Tag:Suites
Voir aussi:
Quelques devoirs
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, suite auxiliaire géométrique
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, suite auxiliaire géométrique
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, convergence monotone et point fixe
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, convergence monotone et point fixe
maison sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, suite auxiliaire arithmétique, convergence monotone et point fixe
