Taux de vasopressine dans le sang
Exercice corrigé - Spécialité maths, terminale générale
Taux de vasopressine
La vasopressine est une hormone favorisant la réabsorption de l'eau par l'organisme. Le taux de vasopressine dans le sang est considéré normal s'il est inférieur à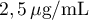 .
.
Cette hormone est sécrétée dès que le volume sanguin diminue. En particulier, il y a production de vasopressine suite à une hémorragie.
On utilisera dans la suite la modélisation suivante: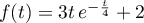 , avec
, avec  .
.
où représente le taux de vasopressine (en
représente le taux de vasopressine (en 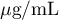 )
dans le sang en fonction du temps t
(en minute) écoulé après le début d'une hémorragie.
)
dans le sang en fonction du temps t
(en minute) écoulé après le début d'une hémorragie.
La vasopressine est une hormone favorisant la réabsorption de l'eau par l'organisme. Le taux de vasopressine dans le sang est considéré normal s'il est inférieur à
Cette hormone est sécrétée dès que le volume sanguin diminue. En particulier, il y a production de vasopressine suite à une hémorragie.
On utilisera dans la suite la modélisation suivante:
où
-
- Quel est le taux de vasopressine dans le sang à l'instant
 ?
?
- Justifier que douze secondes après une hémorragie, le taux de vasopressine dans le sang n'est pas normal.
- Déterminer la limite de la fonction
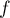 en
en 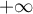 .
On pourra poser
.
On pourra poser 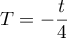 .
.
Interpréter ce résultat.
- Quel est le taux de vasopressine dans le sang à l'instant
- Vérifier que pour tout nombre réel
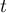 positif:
positif:
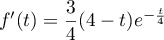 .
.
-
- Étudier le sens de variation de
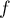 sur l'intervalle
sur l'intervalle
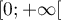 et dresser le tableau de variations de la fonction
et dresser le tableau de variations de la fonction 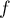 .
.
- À quel instant le taux de vasopressine est-il maximal ?
Quel est alors ce taux ? On en donnera une valeur approchée à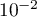 près.
près.
- Étudier le sens de variation de
-
- Démontrer qu'il existe une unique valeur
![$t_0\in [0 ; 4]$](/Generateur-Devoirs/TS/ChapExponentielle/exvasopressine/16.png) telle que
telle que 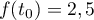 .
.
Donner un encadrement à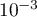 près de
près de 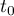 .
.
- On admet qu'il existe une unique valeur
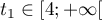 vérifiant
vérifiant 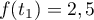 .
.
On en donne une valeur approchée: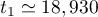 .
.
Déterminer pendant combien de temps, à la seconde près, chez une personne victime d'une hémorragie, le taux de vasopressine reste supérieur à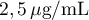 dans le sang.
dans le sang.
- Démontrer qu'il existe une unique valeur
-
- Déterminer l'équation la tangente
 en
en  de la courbe
de la courbe
- Tracer dans un repère la courbe
 ,
avec sa tangente
,
avec sa tangente 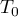 ainsi que ses asymptotes éventuelles.
ainsi que ses asymptotes éventuelles.
- Déterminer l'équation la tangente
Correction
Cacher la correction
-
- À l'instant
 , le taux de vasopressine dans le sang
est
, le taux de vasopressine dans le sang
est 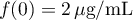 .
.
- Douze secondes après une hémorragie, le taux
de vasopressine est
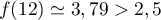 ,
et ce taux n'est donc pas normal.
,
et ce taux n'est donc pas normal.
- Déterminer la limite de la fonction
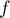 en
en 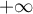 .
Soit
.
Soit  , et alors
, et alors
 ,
et avec ce changement de variable, on a
,
et avec ce changement de variable, on a
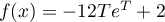 .
.
On a alors, par croissances comparées,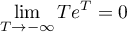 et alors,
et alors,
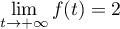 .
.
On en déduit que la droite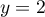 est asymptote horizontale à
est asymptote horizontale à
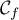 en
en 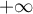 , c'est-à-dire aussi que le taux
de vasopressine tend, "longtemps" après l'hémorragie vers sa valeur
normale de
, c'est-à-dire aussi que le taux
de vasopressine tend, "longtemps" après l'hémorragie vers sa valeur
normale de 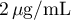 .
.
- À l'instant
- On a
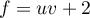 ,
avec
,
avec 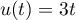 donc
donc 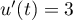 , et
, et  avec
avec 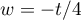 donc
donc 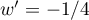 et alors
et alors 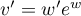 soit
soit
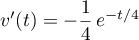 .
.
On obtient alors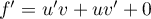 ,
soit
,
soit
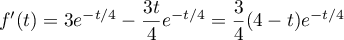 .
.
-
- On en déduit alos le tableau de signe et de variation:
![\[\begin{tabular}{|c|ccccc|}\hline
$t$ & 0 &&4&&$+\infty$\\\hline
$4-t$&&$+$&\zb&$-$&\\\hline
$e^{-t/4}$&&$+$&$|$&$+$&\\\hline
$f'(t)$&&$+$&\zb&$-$&\\\hline
&&&$\frac{12}e+2$&&\\
$f$&&\Large{$\nearrow$}&&\Large{$\searrow$}&\\
&2&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/exvasopressine_c/25.png)
- Le taux de vasopressine est-il maximal à
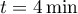 ,
avec
,
avec 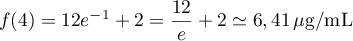 .
.
- On en déduit alos le tableau de signe et de variation:
-
- Sur
![$[0 ; 4]$](/Generateur-Devoirs/TS/ChapExponentielle/exvasopressine_c/28.png) ,
, 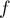 est continue, strictement croissante,
avec
est continue, strictement croissante,
avec 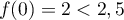 et
et 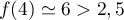 .
.
On en déduit, d'après le théorème de la bijection (ou théorème des valeurs intermédiaires) que l'équation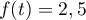 admet une unique solution
admet une unique solution
![$t_0\in[0;4]$](/Generateur-Devoirs/TS/ChapExponentielle/exvasopressine_c/33.png) .
.
On trouve, à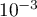 ,
, 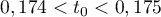 .
.
- On admet qu'il existe une unique valeur
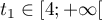 vérifiant
vérifiant 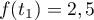 .
.
On en donne une valeur approchée: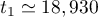 .
.
Déterminer pendant combien de temps, à la seconde près,
Chez une personne victime d'une hémorragie, le taux de vasopressine reste donc supérieur à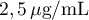 dans le sang
pendant
dans le sang
pendant 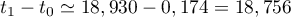 , soit
environ 18 min et 45 s.
, soit
environ 18 min et 45 s.
- Sur
-
- Une équation la tangente
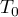 en
en  est
est
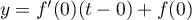 ,
avec
,
avec 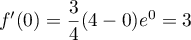 ,
et
,
et 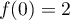 ,
et donc l'équation
,
et donc l'équation
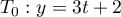 .
.
-
{0}
\psplot[plotpoints=200,linewidth=1.6pt]{0}{30}{3 x mul 2.718 x -4 div exp mul 2 add}\rput(13,4){$\mathcal{C}_f$}
\psline(-.5,2)(.5,2)\rput[r](-.5,2){2}
\psline[linestyle=dashed](4,0)(4,6.41)(0,6.41)
\rput(4,-.3){4}
\psline[linecolor=blue](-1,2)(30,2)\rput(12,1.7){\blue$y=2$}
\psplot[linecolor=red]{-1}{3}{3 x mul 2 add}\rput(2.9,7.6){\red$T_0$}
\psline[linecolor=red]{<->}(1,6.41)(7,6.41)
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapExponentielle/exvasopressine_c/47.png)
- Une équation la tangente
Cacher la correction
Tag:Exponentielle
Voir aussi:
