Révisions de géométrie dans le plan
Exercice corrigé - Spécialité maths, terminale générale
Dans le plan rapporté à un repère orthonormal
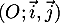 , on considère les points
, on considère les points
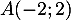 et
et 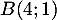 , et la droite
, et la droite
 d'équation
d'équation 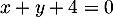 .
.
- Donner une équation cartésienne de la droite
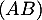 .
.
- Donner une équation cartésienne de la droite
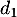 parallèle à
parallèle à 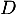 et passant par
et passant par 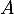 .
.
- Donner une équation cartésienne de la droite
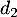 perpendiculaire à
perpendiculaire à 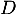 et passant par
et passant par 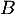 .
.
- Déterminer les coordonnées du point
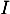 , intersection des droites
, intersection des droites 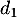 et
et 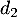 .
.
Correction
Dans le plan rapporté à un repère orthonormal , on considère les points
, on considère les points
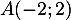 et
et 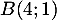 , et la droite
, et la droite
 d'équation
d'équation 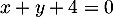 .
.
Cacher la correction
Dans le plan rapporté à un repère orthonormal
- On a
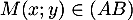 si et seulement si
si et seulement si 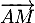 et
et 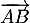 colinéaires,
et donc, avec
colinéaires,
et donc, avec 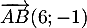 et
et 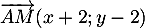 , d'où
, d'où
![\[\begin{array}{ll}M(x;y)\in(AB)&\iff 6(y-2)-(-1)(x+2)=0\\[.3em]
&\iff x+6y-10=0\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/exrvs_c/11.png)
- Un vecteur normal à
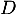 est
est 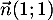 qui est aussi un vecteur normal de
qui est aussi un vecteur normal de 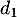 ,
et donc
,
et donc
![\[\begin{array}{ll}M(x;y)\in d_1&\iff \overrightarrow{AM}\cdot\vec{n}_1=0\\[.3em]
&\iff1(x+2)+1(y-2)=0\\[.3em]
&\iff x+y=0\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/exrvs_c/15.png)
-
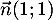 est maintenant un vecteur directeur de
est maintenant un vecteur directeur de 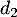 ,
et
,
et 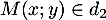 si et seulement si
si et seulement si 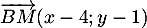 et
et 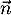 sont colinéaires,
soit
sont colinéaires,
soit
![\[1(x-4)-1(y-1)=0\iff x-y-3=0\]](/Generateur-Devoirs/TS/ChapGeomSpace/exrvs_c/21.png)
- On a
![\[I\in d_1\cap d_2\iff\la\begin{array}{ll}x+y=0\\x-y-3=0\enar\right.\]](/Generateur-Devoirs/TS/ChapGeomSpace/exrvs_c/22.png)
En ajoutant ces deux équations on obtient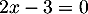 ,
soit
,
soit 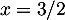 , puis avec la première,
, puis avec la première, 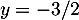 .
.
Finalement, on a obtenu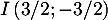 .
.
Cacher la correction
Tag:Géométrie dans l'espace
Voir aussi:
Quelques devoirs
maison de géométrie plane: géométrie plane analytique, vecteurs et équations de droites, exponentielle, tangente
géométrie plane analytique, vecteurs et équations de droites, géométrie avec une hyperbole et ses tangentes, courbe représentative de la fonction inverse
géométrie dans l'espace, vecteurs et équations de plan, représentation paramétrique d&une droite de l'espace, tangente à une courbe, exponentielle
géométrie dans l'espace, vecteurs et équations de plan, représentation paramétrique d&une droite de l'espace, tangente à une courbe, exponentielle - Analyse: étude d'une fonction: variations, limites, TVI, asymptotes, ...
étude de la convexité de fonctions (et variations, tangentes, limites, ...) et géométrie dans l'espace
