Publicité incitative
Exercice corrigé - Spécialité maths, terminale générale
La publicité d'un jeu annonce que la probabilité de gagner est de une chance sur 50 et "ainsi, que tout joueur tentant sa chance régulièrement chaque semaine gagne en moins d'un an !".
- Calculer la probabilité pour un tel joueur, jouant donc régulièrement
chaque semaine pendant un an, de gagner au moins une fois à ce jeu.
Que penser de cette publicité ? - Combien de semaines consécutives devrais-je jouer pour avoir une probabilité de gagner au moins une fois supérieure à 99% ?
Correction
Cacher la correction
- On répète
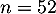 fois (52 semaines dans une année) l'expérience
aléatoire "jouer à ce jeu", dont le succès est d'y gagner avec la probabilité
fois (52 semaines dans une année) l'expérience
aléatoire "jouer à ce jeu", dont le succès est d'y gagner avec la probabilité
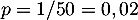 .
On peut raisonnablement supposer ces répétitions identiques et indépendantes,
et on note
.
On peut raisonnablement supposer ces répétitions identiques et indépendantes,
et on note  la variable aléatoire égale au nombre de succès.
la variable aléatoire égale au nombre de succès.
On sait alors que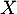 suit la loi binomiale de paramètres
suit la loi binomiale de paramètres 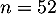 et
et 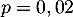 ,
et donc que la probabilité de gagner au moins une fois est
,
et donc que la probabilité de gagner au moins une fois est
![\[P(X\geq1)=1-P(X=0)=1-0,98^{52}\simeq 0,65 = 65\%\]](/Generateur-Devoirs/TS/ChapProbabilites/pub_c/7.png)
La probabilité de gagner en moins d'un an est au plus de 65%, et donc tout joueur ne gagne pas en moins d'un an: l'annonce est fausse. - On cherche cette fois le nombre
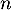 de jours.
De même que précédemment,
de jours.
De même que précédemment, 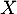 suit la loi binomiale de paramètres
suit la loi binomiale de paramètres
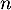 et
et 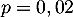 , et la probabilité de gagner au moins une fois en
, et la probabilité de gagner au moins une fois en 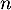 jours
est
jours
est
![\[P(X\geq1)=1-P(X=0)=1-0,98^n\]](/Generateur-Devoirs/TS/ChapProbabilites/pub_c/13.png)
On cherche donc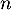 tel que
tel que
![\[\begin{array}{rl}P(X\geq1)=1-0,98^n\geq0,99
\iff&0,98^n\leq1-0,99=0,01\\
\iff&n\ln(0,98)\leq\ln(0,01)\\
\iff&n\geq\dfrac{\ln(0,01)}{\ln(0,98)}\enar\]](/Generateur-Devoirs/TS/ChapProbabilites/pub_c/15.png)
car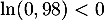 .
.
On trouve donc
![\[n\geq\dfrac{\ln(0,01)}{\ln(0,98)}\simeq227,9\]](/Generateur-Devoirs/TS/ChapProbabilites/pub_c/17.png)
et donc, il faudrait jouer au moins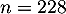 semaines consécutives, soit environ quatre ans et demi.
semaines consécutives, soit environ quatre ans et demi.
Cacher la correction
Tags:ProbabilitésLogarithme
Voir aussi:
Quelques devoirs
Bac blanc: QCM: fonctions, convexité, suite et programme Python - Probabilités: test pour détecter une maladie - Suites: un peu sur les suites - Géométrie dans l'espace - Fonction logarithme
probabilités, loi binomiale et suites de probabilités - suites numériques
Fonction exponentielle - Géométrie dans l'espace - Probabilités, loi binomiale et arbre pondéré - Suite récurrente et python
Bac 2013, Amérique du Sud - Bac 2011, Amérique du nord
sur les probabilités: indépendance d'événements, arbre et probabilités conditionnelles, et le logarithme népérien (ln)
