Position relative, convexité
Exercice corrigé - Spécialité maths, terminale générale
On considère la fonction 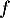 définie sur
définie sur 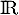 par
par 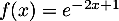 ,
et la droite
,
et la droite 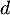 d'équation
d'équation 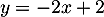 .
.
On cherche à déterminer la position relative de la courbe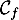 représentative de
représentative de 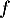 et de la droite
et de la droite 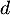 .
.
On cherche à déterminer la position relative de la courbe
- On note
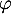 la fonction définie sur
la fonction définie sur 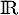 par
par 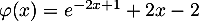 .
.
- Montrer que la fonction
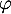 est convexe sur
est convexe sur 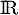 .
.
- Donner une équation de la tangente à la courbe de
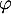 au point d'abscisse
au point d'abscisse  .
.
- Montrer que la fonction
- En utilisant les résultats précédents, donner le signe de
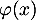 .
.
- Dresser le tableau de variation de
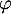 , puis retrouver le résultat
de la question précédente.
, puis retrouver le résultat
de la question précédente.
- Conclure.
Correction
On considère la fonction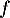 définie sur
définie sur 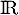 par
par 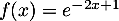 ,
et la droite
,
et la droite 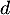 d'équation
d'équation 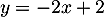 .
.
On cherche à déterminer la position relative de la courbe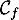 représentative de
représentative de 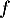 et de la droite
et de la droite 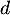 .
.
Cacher la correction
On considère la fonction
On cherche à déterminer la position relative de la courbe
- On note
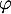 la fonction définie sur
la fonction définie sur 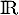 par
par 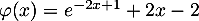 .
.
- On a
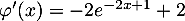 ,
puis
,
puis 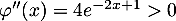 ,
d'où
,
d'où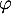 est convexe sur
est convexe sur 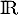 .
.
- Une équation de la tangente à la courbe de
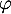 au point d'abscisse
au point d'abscisse  est
est
![\[T:y=\varphi'\lp\dfrac12\rp\lp x-\dfrac12\rp+\varphi\lp\dfrac12\rp\]](/Generateur-Devoirs/TS/ChapExponentielle/exPRcvx_c/18.png)
avec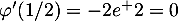 et
et 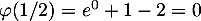 ,
on trouve donc l'équation
,
on trouve donc l'équation 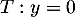 .
.
- On a
- Comme
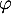 est convexe, sa courbe est au-dessus de ses tangentes,
en particulier au-dessus de
est convexe, sa courbe est au-dessus de ses tangentes,
en particulier au-dessus de 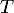 , ce qui s'écrit aussi que
, ce qui s'écrit aussi que
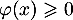 pour tout réel
pour tout réel 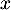 .
.
En d'autres termes,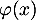 est positif sur
est positif sur 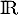 .
.
- On a vu que
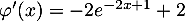 ,
et donc
,
et donc
![\[\begin{array}{ll}\varphi'(x)>0\iff-2e^{-2x+1}+2>0\\
\iff -2e^{-2x+1}>-2\\
\iff e^{-2x+1}<1=e^0\\
\iff -2x+1<0\enar\]](/Generateur-Devoirs/TS/ChapExponentielle/exPRcvx_c/29.png)
car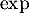 est strictement croissante sur
est strictement croissante sur 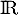 ,
et on obtient donc finalement
,
et on obtient donc finalement
![\[\varphi'(x)>0\iff x>1/2\]](/Generateur-Devoirs/TS/ChapExponentielle/exPRcvx_c/32.png)
d'où le tableau de variation
![\[\begin{tabular}{|c|ccccc|}\hline
$x$&$-\infty$&&$1/2$&&$+\infty$\\\hline
$\varphi'(x)$ && $-$&0&$+$&\\\hline
&&&&&\\
$f$ &&\Large{$\searrow$}&&\Large{$\nearrow$}&\\
&&&0&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/exPRcvx_c/33.png)
avec le minimum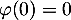 .
.
On retrouve ainsi que pour tout réel
pour tout réel 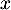 ,
c'est-à-dire que
,
c'est-à-dire que 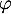 est positive.
est positive.
- Comme on a
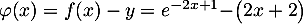 ,
le signe de
,
le signe de 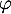 nous donne la position relative de la courbe de
nous donne la position relative de la courbe de 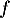 et de la droite
et de la droite 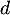 :
: 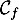 est toujours au-dessus de
est toujours au-dessus de 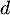 .
.
Cacher la correction
Tags:ExponentielleConvexité
Voir aussi:
Quelques devoirs
maison de géométrie plane: géométrie plane analytique, vecteurs et équations de droites, exponentielle, tangente
géométrie dans l'espace, vecteurs et équations de plan, représentation paramétrique d&une droite de l'espace, tangente à une courbe, exponentielle
Bac blanc: QCM: fonctions, convexité, suite et programme Python - Probabilités: test pour détecter une maladie - Suites: un peu sur les suites - Géométrie dans l'espace - Fonction logarithme
logarithme népérien: résolution d'équations, étude de fonction, et convexité, points d'inflexion
maison: calculs de dérivées, limites, fonctions et suites récurrentes, démonstration par récurrence et théorème des gendarmes
