Oral de Bac - Variations, limites et TVI
Exercice corrigé - Spécialité maths, terminale générale
Soit  la fonction définie sur
la fonction définie sur ![$]0;+\infty[](/Generateur-Devoirs/TS/ChapLogarithme/exOral03/2.png) par
par 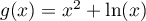 .
.
- Dresser le tableau de variation de
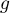 . Préciser les limites.
. Préciser les limites.
- Montrer que l'équation
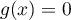 admet une unique solution
admet une unique solution
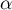 .
.
Donner un encadrement de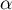 d'amplitude
d'amplitude 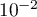 .
.
- Soit
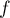 la fonciton définie
la fonciton définie ![$]0;+\infty[](/Generateur-Devoirs/TS/ChapLogarithme/exOral03/10.png) par
par
 .
.
Montrer que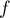 admet un minimum en
admet un minimum en  .
.
Correction
Cacher la correction
- Pour tout
 ,
, 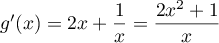 .
.
Pour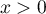 , on
, on 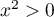 , donc
, donc  , et ainsi,
, et ainsi, 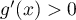 , et
, et
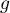 est strictement croissante sur
est strictement croissante sur  .
.
En 0: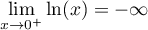 , et donc
, et donc
 .
.
En :
:
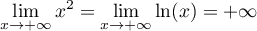 ,
donc, par addition des limites:
,
donc, par addition des limites:
 .
.
![\begin{tabular}{|c|ccc|}\hline
$x$ & $0$ &\qquad\qquad& $+\infty$ \\\hline
$g'(x)$ & & $+$ &\\\hline
&&&$+\infty$\\
$g$ && \psline[arrowsize=7pt]{->}(-.6,-.4)(.6,.4)&\\
&$-\infty$&&\\\hline
\end{tabular}](/Generateur-Devoirs/TS/ChapLogarithme/exOral03_c/14.png)
-
 est continue, strictement croissante sur
est continue, strictement croissante sur ![$]0;+\infty[](/Generateur-Devoirs/TS/ChapLogarithme/exOral03_c/16.png) ,
avec
,
avec 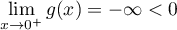 et
et 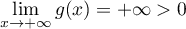 ,
donc, d'après le théorème de la bijection
(ou corollaire du théorème des valeurs intermédiaires)
il existe une unique solution
,
donc, d'après le théorème de la bijection
(ou corollaire du théorème des valeurs intermédiaires)
il existe une unique solution 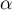 à l'équation
à l'équation 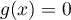 .
.
A la calculatrice, on a et
et  , ce qui montre que
, ce qui montre que 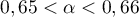 .
.
- Pour tout
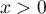 ,
, 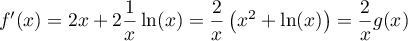 .
.
![\begin{tabular}{|c|ccc|}\hline
$x$ & $0$ &\qquad$\alpha$\qquad\qquad& $+\infty$ \\\hline
&&&$+\infty$\\
$g$ && 0\psline[arrowsize=7pt]{->}(-1,-.4)(1,.4)&\\
&$-\infty$&&\\\hline
$g(x)$ && $-$ \qquad \zb\qquad $+$& \\\hline
$f'(x)$ && $-$ \qquad \zb\qquad $+$& \\\hline
&&&\\
$f$ &&\psline[arrowsize=7pt]{->}(-1.4,.4)(-.4,-.4)&
\psline[arrowsize=7pt]{->}(-1.4,-.4)(-.4,.4)\\
&&$f(\alpha)$&\\\hline
\end{tabular}](/Generateur-Devoirs/TS/ChapLogarithme/exOral03_c/26.png)
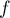 admet donc bien un minimum en
admet donc bien un minimum en 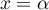 .
.
Cacher la correction
Tag:Logarithme
Voir aussi:
