Oral de Bac: suite recurrente, fonction, récurrence et convergence monotone
Exercice corrigé - Spécialité maths, terminale générale
On définit la suite 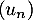 par
par 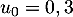 et, pour tout entier
et, pour tout entier 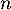 ,
par
,
par 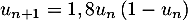 .
.
- Etudier les variations de la fonction
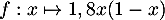 sur
sur ![$[0;1]$](/Generateur-Devoirs/TS/ChapSuites/exOral05/6.png) et montrer que
et montrer que 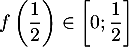 .
.
- Démontrer par récurrence que, pour tout entier
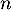 ,
,
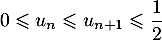 .
.
- En déduire que la suite
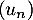 converge.
converge.
- Déterminer la limite de la suite
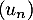 .
.
Correction
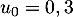 et
et 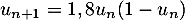 .
.
Cacher la correction
-
Pour tout ![$x\in[0;1]$](/Generateur-Devoirs/TS/ChapSuites/exOral05_c/3.png) ,
, 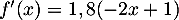 .
.
De plus,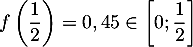 .
.
![\[\begin{tabular}{|c|ccccc|}\hline
$x$ & $0$ && $\dfrac12$ && 1 \\\hline
$-2x+1$ && $+$ & \mbox{$0\hspace{-0.67em}\mid$} & $-$ & \\\hline
$f'(x)$ && $+$ & \mbox{$0\hspace{-0.67em}\mid$} & $-$ & \\\hline
&&&$0,45$&& \\
$f$&& \Large{$\nearrow$}& &\Large{$\searrow$} &\\
&0&&&&0 \\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapSuites/exOral05_c/6.png)
-
Initialisation: Pour ,
,
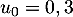 et
et 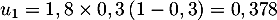 .
On a bien ainsi
.
On a bien ainsi 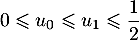 .
Hérédité: Supposons que pour un entier
.
Hérédité: Supposons que pour un entier 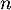 , on ait
, on ait
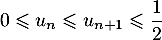 .
Comme la fonction
.
Comme la fonction 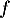 est croissante sur
est croissante sur
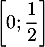 , on a donc
, on a donc
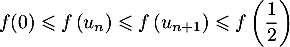 .
.
Or,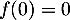 ,
, 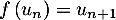 ,
,
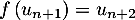 et
et 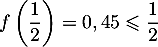 .
Ainsi,
.
Ainsi, 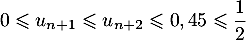 ,
et la propriété est encore vraie au rang
,
et la propriété est encore vraie au rang 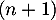 .
Conclusion: D'après le principe de récurrence,
pour tout entier
.
Conclusion: D'après le principe de récurrence,
pour tout entier 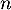 ,
,
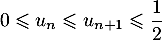 .
.
- La suite
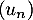 est donc croissante est majorée par
est donc croissante est majorée par  .
On en déduit qu'elle converge vers une limite
.
On en déduit qu'elle converge vers une limite 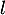 .
.
- La limite
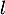 vérifie nécessairement, d'après le théorème du point fixe,
vérifie nécessairement, d'après le théorème du point fixe,
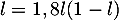

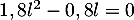

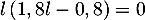
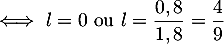 .
.
Or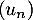 est croissante avec
est croissante avec 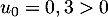 , et donc, pour tout
entier
, et donc, pour tout
entier 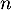 ,
,  .
La limite de la suite ne peut donc être que
.
La limite de la suite ne peut donc être que 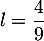 .
.
Cacher la correction
Tag:Suites
Voir aussi:
