Oral de Bac - Position relative de droites dans l'espace, représentations paramétriques
Exercice corrigé - Spécialité maths, terminale générale
Dans l'espace muni du repère orthonormal 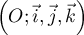 on considère les droites
on considère les droites 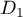 ,
, 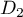 et
et 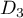 de représentations paramétriques:
de représentations paramétriques:
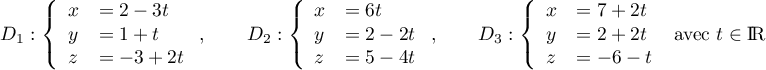
Etudier la position relative des droites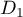 et
et 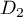 , puis
, puis 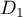 et
et 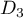 ,
et enfin
,
et enfin 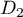 et
et 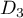 .
.
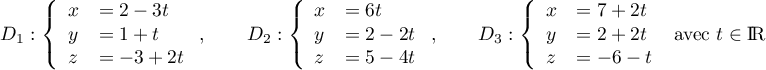
Etudier la position relative des droites
Correction
Le vecteur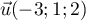 est un vecteur directeur de
est un vecteur directeur de 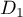 .
.
Le vecteur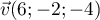 est un vecteur directeur de
est un vecteur directeur de 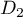 .
.
Les vecteurs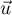 et
et 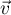 sont colinéaires,
car
sont colinéaires,
car 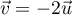 , et les droites
, et les droites 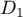 et
et 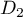 sont donc parallèles.
sont donc parallèles.
Elles peuvent être confondues ou strictement parallèles.
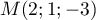 est un point de
est un point de 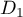 .
Dans la représentation paramétrique de
.
Dans la représentation paramétrique de 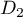 :
:
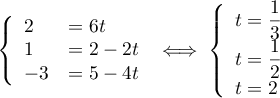
ce qui est impossible est montre donc que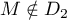 .
Ainsi,
.
Ainsi, 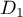 et
et 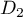 sont strictement parallèles.
sont strictement parallèles.
Le vecteur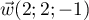 est un vecteur directeur de
est un vecteur directeur de 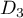 .
Comme
.
Comme 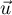 et
et 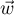 ne sont pas colinéaires, les droites
ne sont pas colinéaires, les droites
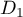 et
et 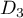 ne sont pas parallèles.
ne sont pas parallèles.
Soit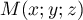 un éventuel point commun à
un éventuel point commun à 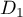 et
et 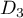 , alors
alors il existe deux réels
, alors
alors il existe deux réels 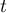 et
et 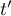 tels que
tels que
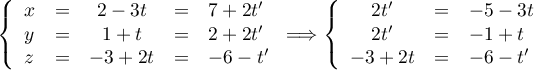
Les deux premières équations donnent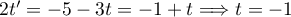 ,
et donc,
,
et donc, 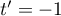 . La dernière équation est aussi vérifiée.
. La dernière équation est aussi vérifiée.
Ces deux droites sont donc sécantes en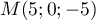 .
.
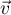 et
et 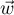 ne sont pas colinéaires et les droites
ne sont pas colinéaires et les droites 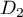 et
et
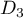 ne sont donc pas parallèles.
On cherche de même que précédemment un point d'intersection
ne sont donc pas parallèles.
On cherche de même que précédemment un point d'intersection
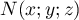 :
:
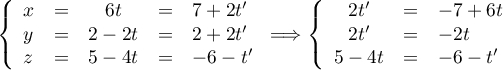
Les deux premières équations donnent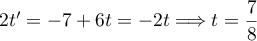 et donc
et donc 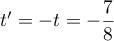 .
.
Par contre la dernière équation n'est pas vérifiée: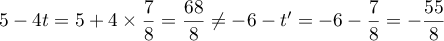 ,
et il n'existe donc pas de réels
,
et il n'existe donc pas de réels 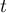 et
et 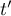 ;
les droites
;
les droites 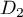 et
et 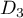 ne sont pas sécantes.
ne sont pas sécantes.
Cacher la correction
Le vecteur
Le vecteur
Les vecteurs
Elles peuvent être confondues ou strictement parallèles.
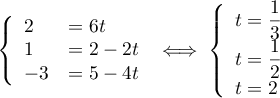
ce qui est impossible est montre donc que
Le vecteur
Soit
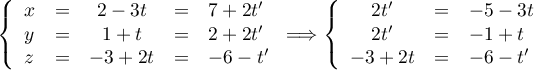
Les deux premières équations donnent
Ces deux droites sont donc sécantes en
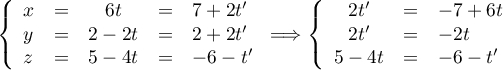
Les deux premières équations donnent
Par contre la dernière équation n'est pas vérifiée:
Cacher la correction
Tag:Géométrie dans l'espace
Voir aussi:
