Logarithme et convexité
Exercice corrigé - Spécialité maths, terminale générale
On considère la fonction 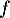 définie sur
définie sur ![$]0;+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex-ln-cvx/2.png) par
par
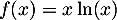 , et on note
, et on note 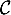 sa courbe représentative.
sa courbe représentative.
- Montrer que la fonction
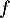 est convexe sur
est convexe sur ![$]0;+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex-ln-cvx/6.png) .
.
- Donner l'équation de la tangente à
 au point d'abscisse 1.
au point d'abscisse 1.
- Montrer que, pour tout
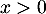 , on a
, on a
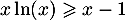 .
.
Correction
Cacher la correction
- On a
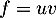 avec
avec 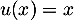 , donc
, donc  et
et 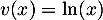 donc
donc 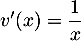 , et alors
, et alors
 , soit
, soit
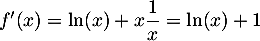 .
.
Ensuite, on a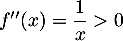 pour
pour 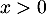 ,
ce qui montre que
,
ce qui montre que 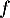 est convexe sur
est convexe sur ![$]0;+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex-ln-cvx_c/11.png) .
.
- La tangente a pour équation
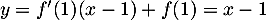 .
.
- Comme
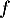 est convexe, sa courbe est au-dessus de ses tangentes,
en particulier au-dessus de la tangente en 1, c'est-à-dire que,
pour tout
est convexe, sa courbe est au-dessus de ses tangentes,
en particulier au-dessus de la tangente en 1, c'est-à-dire que,
pour tout 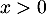 , on a
, on a 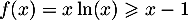 .
.
Cacher la correction
Tags:LogarithmeConvexité
Voir aussi:
