Inégalité (de cours) avec une exponentielle
Exercice corrigé - Spécialité maths, terminale générale
Montrer que, pour tout 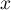 réel,
réel, 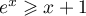 .
.
On pourra étudier les variations de la fonction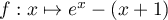 .
.
On pourra étudier les variations de la fonction
Correction
Soit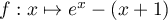 , définie sur
, définie sur 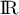 .
.
On a alors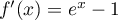 et alors
et alors
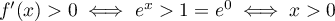 car la fonction exponentielle est strictement croissante sur
car la fonction exponentielle est strictement croissante sur 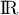 .
On a ainsi le tableau de variation
.
On a ainsi le tableau de variation
![\[\begin{tabular}{|c|ccccc|}\hline
$x$ &$-\infty$ && 1 && $+\infty$ \\\hline
$f'(x)$ && $-$ &0& $+$ &\\\hline
&&&&&\\
$f$&&\Large{$\searrow$}&&\Large{$\nearrow$}&\\
&&&0&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex00_c/6.png)
avec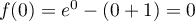 .
.
Ainsi, le minimum de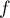 sur
sur 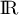 est
est 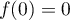 ,
et en particulier, pour tout réel
,
et en particulier, pour tout réel 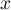 , on a
, on a
![\[\begin{array}{ll}f(x)\geqslant f(0)=0
&\iff e^x-(x+1)\geqslant0\\
&\iff e^x\geqslant x+1\enar\]](/Generateur-Devoirs/TS/ChapExponentielle/ex00_c/12.png)
Cacher la correction
Soit
On a alors
![\[\begin{tabular}{|c|ccccc|}\hline
$x$ &$-\infty$ && 1 && $+\infty$ \\\hline
$f'(x)$ && $-$ &0& $+$ &\\\hline
&&&&&\\
$f$&&\Large{$\searrow$}&&\Large{$\nearrow$}&\\
&&&0&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex00_c/6.png)
avec
Ainsi, le minimum de
Cacher la correction
Tag:Exponentielle
Voir aussi:
