Fonction exponentielle à identifier et à étudier
Exercice corrigé - Spécialité maths, terminale générale
On considère les points  et
 et la droite  d'équation
 .
On note  la fonction définie sur  dont la courbe
représentative, notée  est donnée ci-contre.
 et  tels que:
|
 |
, 
.
et 
appartiennent à la
courbe 
.
-
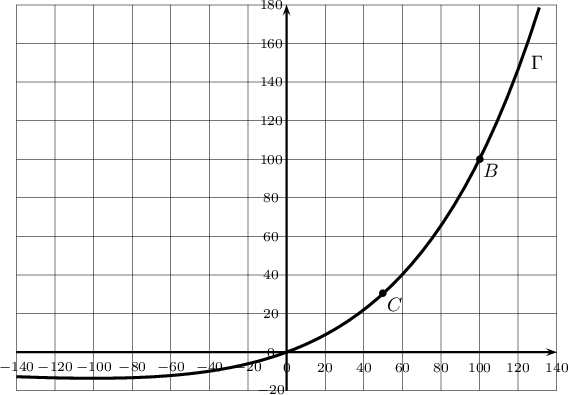- Montrer que le couple
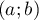est solution du système:
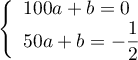
- En déduire que, pour tout réel
,
.
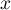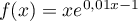- Montrer que le couple
- Déterminer la limite de
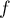en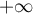 
.
-
- Montrer que pour tout réel
,
.
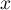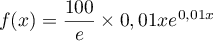- En déduire le limite de
en 
.
- Montrer que pour tout réel
- Etudier les variations de
.
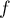On donnera le tableau de variations complet.
- Etudier la position relative de la courbe
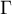et de la
droite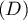 
.
Correction
Cacher la correction
-
-
Ainsi, le couple
est bien solution du système:
- On résout le système précédent.
En soustrayant ces deux équations, on obtient
.
De même, en multipliant la deuxième équation par 2, et en soustrayant les deux équations, on obtient
, soit 
.
On en déduit l'expression de
:
.
-
-
,
et 
.
Ainsi, par composition des limites,
.
Comme
, on trouve, par produit des
limites, que
,
-
- Pour tout réel
,
.
- Soit
,
alors
, car l'exponentielle est prépondérante en 
devant
.
Ainsi, 
.
- Pour tout réel
- Pour tout réel
,
.
Pour tout réel
, 
, d'où
- Pour tout réel
,
.
Or,
, car la fonction exponentielle est strictement
croissante sur 
,
et ainsi,
.
On en déduit:
Ainsi, sur
,
est au-dessus de 
,
tandis que sur 
,
est au-dessous de 
.
Enfin, 
et 
se coupent aux points
de coordonnées 
et 
.
Cacher la correction
Tag:Exponentielle
Autres sujets au hasard:
Voir aussi: