Étude complète de fonction
Exercice corrigé - Spécialité maths, terminale générale
On considère la fonction 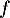 définie par l'expression
définie par l'expression  .
.
On note sa courbe représentative.
sa courbe représentative.
Dresser le tableau de variation de .
Préciser toutes les limites de
.
Préciser toutes les limites de  .
.
Tracer l'allure de en utilisant tous les résultats précédants.
en utilisant tous les résultats précédants.
On note
Dresser le tableau de variation de
Tracer l'allure de
Correction
C'est le signe de la dérivée de f qui nous donne son sens de variation. Ici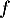 est la somme d'une fonction affine (que l'on dérive facilement) et de
est la somme d'une fonction affine (que l'on dérive facilement) et de
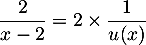 avec
avec  dont la dérivée est
dont la dérivée est 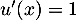 .
.
La dérivée de étant
étant 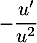 , on trouve donc que
, on trouve donc que
 .
.
Pour pouvoir déterminer le signe de cette expression, on l'exprime sur un seul dénominateur:
![\[f'(x)=\dfrac{2(x-2)^2-2}{(x-2)^2}=\dfrac{2x^2-8x+6}{(x-2)^2}=2\dfrac{x^2-4x+3}{(x-2)^2}\]](/Generateur-Devoirs/TS/ChapFonctions/exEF_c/8.png)
Le numérateur est un trinôme du second degré dont le discriminant est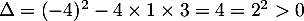 et qui admet donc deux racines
et qui admet donc deux racines
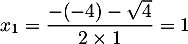 et
et 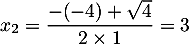 .
.
On obtient alors le signe du trinôme, et donc de la dérivée, et enfin le sens de variation de (on n'oublie pas non plus la valeur interdite…).
(on n'oublie pas non plus la valeur interdite…).
![\[\begin{tabular}{|c|lcccccccr|}\hline
$x$&$-\infty$&&1&&2&&3&&$+\infty$\\\hline
$x^2-4x+3$ &&$+$&0&$-$&$|$&$-$&0&$+$&\\\hline
$(x-2)^2$ &&$+$&$|$&$+$&0&$+$&$|$&$+$&\\\hline
$f'(x)$ &&$+$&0&$-$&&$-$&0&$+$&\\\hline
&&&2&&&$+\infty$&&&$+\infty$\\
$f$&&\Large{$\nearrow$}&&\Large{$\searrow$}&
\psline(0,-.6)(0,1.3)\psline(.07,-.6)(.07,1.3)&
\Large{$\searrow$}&&\Large{$\nearrow$}&\\
&$-\infty$&&&$-\infty$&&&9&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapFonctions/exEF_c/13.png)
Limites de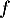 :
En l'infini, on a
:
En l'infini, on a
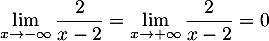 et
et
 et
et
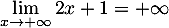 .
.
On obtient alors, par somme des limites,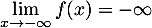 et
et

Lorsque , on
, on 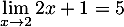 ,
et
,
et 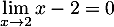 .
.
Le quotient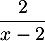 tend vers l'infini, et il reste à déterminer son signe en séparant les cas
tend vers l'infini, et il reste à déterminer son signe en séparant les cas  et
et  :
:
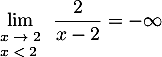 et donc
et donc
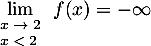 .
.
On trouve de même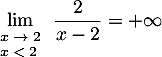 et donc
et donc
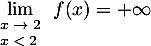 .
.
On en déduit de plus que la droite d'équation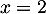 est une asymptote verticale à
est une asymptote verticale à 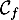 .
.
{\i}}
\psplot{-3}{1.9}{2 x mul 1 add 2 x 2 sub div add}
\psplot{2.1}{5}{2 x mul 1 add 2 x 2 sub div add}
\psline[linecolor=blue](2,-17)(2,22)
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapFonctions/exEF_c/32.png)
Cacher la correction
C'est le signe de la dérivée de f qui nous donne son sens de variation. Ici
La dérivée de
Pour pouvoir déterminer le signe de cette expression, on l'exprime sur un seul dénominateur:
Le numérateur est un trinôme du second degré dont le discriminant est
On obtient alors le signe du trinôme, et donc de la dérivée, et enfin le sens de variation de
![\[\begin{tabular}{|c|lcccccccr|}\hline
$x$&$-\infty$&&1&&2&&3&&$+\infty$\\\hline
$x^2-4x+3$ &&$+$&0&$-$&$|$&$-$&0&$+$&\\\hline
$(x-2)^2$ &&$+$&$|$&$+$&0&$+$&$|$&$+$&\\\hline
$f'(x)$ &&$+$&0&$-$&&$-$&0&$+$&\\\hline
&&&2&&&$+\infty$&&&$+\infty$\\
$f$&&\Large{$\nearrow$}&&\Large{$\searrow$}&
\psline(0,-.6)(0,1.3)\psline(.07,-.6)(.07,1.3)&
\Large{$\searrow$}&&\Large{$\nearrow$}&\\
&$-\infty$&&&$-\infty$&&&9&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapFonctions/exEF_c/13.png)
Limites de
On obtient alors, par somme des limites,
Lorsque
Le quotient
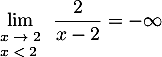 et donc
et donc
On trouve de même
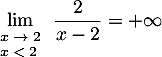 et donc
et donc
On en déduit de plus que la droite d'équation
{\i}}
\psplot{-3}{1.9}{2 x mul 1 add 2 x 2 sub div add}
\psplot{2.1}{5}{2 x mul 1 add 2 x 2 sub div add}
\psline[linecolor=blue](2,-17)(2,22)
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapFonctions/exEF_c/32.png)
Cacher la correction
Tags:Limites de fonctionsFonctions
Voir aussi:
Quelques devoirs
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, suite auxiliaire géométrique
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, suite auxiliaire géométrique
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, convergence monotone et point fixe
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, convergence monotone et point fixe
maison sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, suite auxiliaire arithmétique, convergence monotone et point fixe
