Convexité d'un polynome
Exercice corrigé - Spécialité maths, terminale générale
On considère la fonction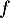 
définie sur 
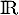par
.
Étudier la convexité de le fonction
.
Préciser les abscisses des éventuels points d'inflexion.
définie sur par
.
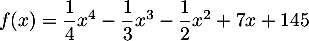Étudier la convexité de le fonction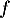
.
Préciser les abscisses des éventuels points d'inflexion.
Correction
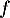est une fonction polynôme et donc, en particulier,
est dérivable deux fois avec
![\[f'(x)=x^3-x^2-x+7\]](/Generateur-Devoirs/TS/ChapFonctions/excvx-poly_c/2.png)
et
![\[f''(x)=3x^2-2x-1\]](/Generateur-Devoirs/TS/ChapFonctions/excvx-poly_c/3.png)
La convexité de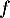
est donnée par le signe de sa dérivée,
qui est une trinôme du second degré de discriminant
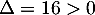et qui admet donc deux racines
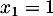et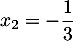 
.
On obtient alors le signe,
![\[\begin{tabular}{|c|ccccccc|}\hline
$x$&$-\infty$&&$-1/3$&&1&&$+\infty$\\\hline
$f''(x)$&&$+$&0&$-$&0&$+$&\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapFonctions/excvx-poly_c/8.png)
et ainsi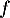
est convexe sur ![$]-\infty;-1/3]\cup[1;+\infty[$](/Generateur-Devoirs/TS/ChapFonctions/excvx-poly_c/10.png)
et concave sur ![$[-1/3;1]$](/Generateur-Devoirs/TS/ChapFonctions/excvx-poly_c/11.png)
.
Enfin, la courbe de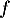
admet deux points d'inflexion,
en 
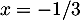et 
.
Cacher la correction
est une fonction polynôme et donc, en particulier,
est dérivable deux fois avec
et
La convexité de
est donnée par le signe de sa dérivée,
qui est une trinôme du second degré de discriminant
et qui admet donc deux racines
et .
On obtient alors le signe,
et ainsi
est convexe sur
et concave sur .
Enfin, la courbe de
admet deux points d'inflexion,
en et .
Cacher la correction
Tag:Convexité
Autres sujets au hasard:
Voir aussi: