Bac 2022 (12 mai): QCM, fonctions, convexité, suites
Exercice corrigé - Spécialité maths, terminale générale
Cet exercice est un questionnaire à choix multiples. Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte. Une réponse fausse, une réponse multiple ou l'absence de réponse à une question ne rapporte ni n'enlève de point.
Pour répondre, indiquer sur la copie le numéro de la question et la lettre de la réponse choisie.
Aucune justification n'est demandée.
Pour les questions 1 à 3 ci-dessous, on considère une fonction définie et deux fois dérivable sur
définie et deux fois dérivable sur 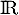 . La courbe de sa fonction dérivée
. La courbe de sa fonction dérivée  est donnée ci-dessous.
est donnée ci-dessous.
On admet que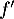 admet un maximum en
admet un maximum en 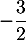 et que sa courbe coupe l'axe des abscisses au point de coordonnées
et que sa courbe coupe l'axe des abscisses au point de coordonnées 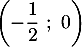 .
.
Question 1 :
a. La fonction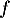 admet un maximum en
admet un maximum en 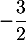
b. La fonction admet un maximum en
admet un maximum en 
c. La fonction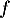 admet un minimum en
admet un minimum en 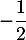
d. Au point d'abscisse , la courbe de la fonction
, la courbe de la fonction 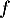 admet une tangente horizontale.
admet une tangente horizontale.
![\[\psset{unit=1.2cm}
\begin{pspicture*}(-5.2,-2.6)(1,1)
\psgrid[gridlabels=0pt,subgriddiv=4,gridwidth=0.25pt,subgridwidth=0.15pt]
\psaxes[linewidth=1.25pt,labelFontSize=\scriptstyle]{->}(0,0)(-5.2,-2.6)(1,1)
%\pscurve[linecolor=blue,linewidth=1.25pt](-5.2,0.05)(-4,0.13)(-3,0.28)(-2,0.4)(-1,0.35)(0,-1)(0.38,-2.6)
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=red]{-5}{3}{2 x mul 1 add 2.71828 x exp mul neg}
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapFonctions/ex12052022/17.png)
Question 2 :
a. La fonction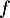 est convexe sur
est convexe sur ![$\left]- \infty~;~- \dfrac32\right[$](/Generateur-Devoirs/TS/ChapFonctions/ex12052022/19.png)
b. La fonction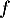 est convexe sur
est convexe sur ![$\left]- \infty;~- \dfrac12\right[$](/Generateur-Devoirs/TS/ChapFonctions/ex12052022/21.png)
c. La courbe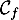 représentant la fonction
représentant la fonction  n'admet pas de point d'inflexion
n'admet pas de point d'inflexion
d. la fonction est concave sur
est concave sur ![$\left] - \infty~;~- \dfrac12\right[$](/Generateur-Devoirs/TS/ChapFonctions/ex12052022/25.png)
Question 3:
La dérivée seconde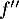 de la fonction
de la fonction 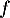 vérifie :
vérifie :
a.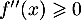 pour
pour ![$x \in \left]-\infty~;~- \dfrac12\right[$](/Generateur-Devoirs/TS/ChapFonctions/ex12052022/29.png)
b. pour
pour ![$x \in [- 2~;~- 1]$](/Generateur-Devoirs/TS/ChapFonctions/ex12052022/31.png)
c.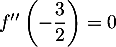
d.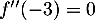
Question 4 :
On considère trois suites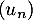 ,
, 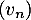 et
et 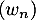 . On sait que, pour tout entier naturel
. On sait que, pour tout entier naturel 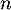 , on a :
, on a : 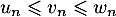 et de plus:
et de plus:  et
et 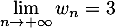 .
.
On peut alors affirmer que :
a. la suite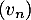 converge
converge
b. Si la suite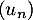 est croissante alors la suite
est croissante alors la suite 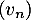 est minorée par
est minorée par 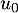
c.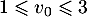
d. la suite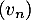 diverge.
diverge.
Question 5:
On considère une suite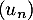 telle que, pour tout entier naturel
telle que, pour tout entier naturel 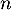 non nul:
non nul: 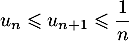 .
.
On peut alors affirmer que :
a. la suite diverge
diverge
b. la suite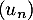 converge
c.
converge
c. d.
d. 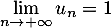 .
.
Question 6:
On considère une suite réelle telle que pour tout entier naturel
une suite réelle telle que pour tout entier naturel 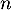 , on a :
, on a : 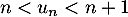 .
.
On peut affirmer que:
a. Il existe un entier naturel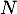 tel que
tel que 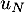 est un entier
est un entier
b. la suite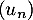 est croissante
est croissante
c. la suite est convergente
est convergente
d. La suite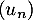 n'a pas de limite.
n'a pas de limite.
Pour répondre, indiquer sur la copie le numéro de la question et la lettre de la réponse choisie.
Aucune justification n'est demandée.
Pour les questions 1 à 3 ci-dessous, on considère une fonction
On admet que
Question 1 :
a. La fonction
b. La fonction
c. La fonction
d. Au point d'abscisse
On rappelle que la courbe ci-dessous représente la fonction dérivée 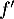 de
de 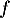 .
.
![\[\psset{unit=1.2cm}
\begin{pspicture*}(-5.2,-2.6)(1,1)
\psgrid[gridlabels=0pt,subgriddiv=4,gridwidth=0.25pt,subgridwidth=0.15pt]
\psaxes[linewidth=1.25pt,labelFontSize=\scriptstyle]{->}(0,0)(-5.2,-2.6)(1,1)
%\pscurve[linecolor=blue,linewidth=1.25pt](-5.2,0.05)(-4,0.13)(-3,0.28)(-2,0.4)(-1,0.35)(0,-1)(0.38,-2.6)
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=red]{-5}{3}{2 x mul 1 add 2.71828 x exp mul neg}
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapFonctions/ex12052022/17.png)
Question 2 :
a. La fonction
b. La fonction
c. La courbe
d. la fonction
Question 3:
La dérivée seconde
a.
b.
c.
d.
Question 4 :
On considère trois suites
On peut alors affirmer que :
a. la suite
b. Si la suite
c.
d. la suite
Question 5:
On considère une suite
On peut alors affirmer que :
a. la suite
b. la suite
Question 6:
On considère
On peut affirmer que:
a. Il existe un entier naturel
b. la suite
c. la suite
d. La suite
Correction
Question 1 : b.
Pour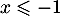 , on a
, on a 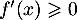 donc
donc 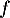 est croissante,
et inversement ensuite pour
est croissante,
et inversement ensuite pour 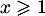 .
.
Ainsi, a un maximum local en
a un maximum local en 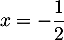 .
.
Question 2 : a.
La dérivée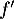 est croissante sur
est croissante sur ![$\left]- \infty~;~- \dfrac32\right[$](/Generateur-Devoirs/TS/ChapFonctions/ex12052022_c/8.png) ,
donc
,
donc 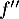 est positive sur cet intervalle, et
est positive sur cet intervalle, et 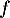 y est convexe.
y est convexe.
Question 3: c.
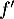 admet un maximum en
admet un maximum en  , donc sa dérivée
, donc sa dérivée  s'y annule.
s'y annule.
Question 4 : b.
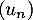 croissante signifie que
croissante signifie que
![\[u_0\leqslant u_1\leqslant u_2\leqslant \dots\leqslant u_n\leqslant\dots\]](/Generateur-Devoirs/TS/ChapFonctions/ex12052022_c/15.png)
et on a donc, pour tout entier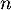 ,
,
![\[u_0\leqslant u_n\leqslant v_n\]](/Generateur-Devoirs/TS/ChapFonctions/ex12052022_c/17.png)
ce qui montre que est minorée par
est minorée par 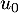 .
.
Question 5: b.
Les inégalités données montrent que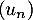 est croissante et aussi aue
est croissante et aussi aue  est majorée, par 1 par exemple, car
est majorée, par 1 par exemple, car
![\[u_n\leqslant u_{n+1}\leqslant\dfrac1n\leqslant1\]](/Generateur-Devoirs/TS/ChapFonctions/ex12052022_c/22.png)
Ainsi est convergente (théorème de convergence monotone)
est convergente (théorème de convergence monotone)
Question 6: b.
On a
![\[n < u_n < n + 1\]](/Generateur-Devoirs/TS/ChapFonctions/ex12052022_c/24.png)
donc, au rang suivant
![\[n+1 < u_{n+1} < n + 2\]](/Generateur-Devoirs/TS/ChapFonctions/ex12052022_c/25.png)
et donc, en particulier
![\[u_n<n+1<u_{n+1}\]](/Generateur-Devoirs/TS/ChapFonctions/ex12052022_c/26.png)
qui montre que la suite est croissante.
Cacher la correction
Question 1 : b.
Pour
Ainsi,
Question 2 : a.
La dérivée
Question 3: c.
Question 4 : b.
et on a donc, pour tout entier
ce qui montre que
Question 5: b.
Les inégalités données montrent que
Ainsi
Question 6: b.
On a
donc, au rang suivant
et donc, en particulier
qui montre que la suite est croissante.
Cacher la correction
Tags:QCMFonctionsSuites
Voir aussi:
