Bac 2022 (12 mai): Arbre et loi binomiale
Exercice corrigé - Spécialité maths, terminale générale
Le coyote est un animal sauvage proche du loup, qui vit en Amérique du Nord.
Dans l'état d'Oklahoma, aux États-Unis, 70 % des coyotes sont touchés par une maladie appelée ehrlichiose.
Il existe un test aidant à la détection de cette maladie. Lorsque ce test est appliqué à un coyote, son résultat est soit positif, soit négatif, et on sait que :
Partie A
Des vétérinaires capturent un coyote d'Oklahoma au hasard et lui font subir un test pour l'ehrlichiose.
On considère les évènements suivants :
On note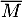 et
et 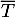 respectivement les évènements contraires de M et T.
respectivement les évènements contraires de M et T.
Partie B
On rappelle que la probabilité qu'un coyote capturé au hasard présente un test positif est de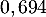 .
.
Dans l'état d'Oklahoma, aux États-Unis, 70 % des coyotes sont touchés par une maladie appelée ehrlichiose.
Il existe un test aidant à la détection de cette maladie. Lorsque ce test est appliqué à un coyote, son résultat est soit positif, soit négatif, et on sait que :
- Si le coyote est malade, le test est positif dans 97 % des cas.
- Si le coyote n'est pas malade, le test est négatif dans 95 % des cas.
Partie A
Des vétérinaires capturent un coyote d'Oklahoma au hasard et lui font subir un test pour l'ehrlichiose.
On considère les évènements suivants :
- M: « le coyote est malade »;
- T: « le test du coyote est positif ».
On note
- Recopier et compléter l'arbre pondéré ci-dessous qui modélise la situation.
![\[\psset{xunit=1.3cm,yunit=1.4cm}
\begin{pspicture}(-.4,-2)(4.2,2)
\psline(0,0)(1.5,1)\rput(1.75,1){$M$}
\rput(.8,.9){\dots}
\rput(.8,-1){\dots}
\psline(0,0)(1.5,-1)\rput(1.75,-1){$\overline{M}$}
\psline(2.1,1.2)(3.5,1.6)\rput(3.8,1.6){$T$}
\rput(2.8,1.7){\dots}
\psline(2.1,.8)(3.5,.4)\rput(3.8,.4){$\overline{T}$}
\rput(2.8,.2){\dots}
\rput(2.8,-.4){\dots}
\psline(2.1,-1.2)(3.5,-1.6)\rput(3.8,-1.6){$\overline{T}$}
\psline(2.1,-.8)(3.5,-.4)\rput(3.8,-.4){$T$}
\rput(2.8,-1.8){\dots}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022/7.png)
- Déterminer la probabilité que le coyote soit malade et que son test soit positif.
- Démontrer que la probabilité de T est égale à
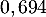 .
.
- On appelle « valeur prédictive positive du test » la probabilité que le coyote soit effectivement malade sachant que son test est positif.
Calculer la valeur prédictive positive du test. On arrondira le résultat au millième. -
- Par analogie avec la question précédente, proposer une définition de la « valeur prédictive négative du test » et calculer cette valeur en arrondissant au millième.
- Comparer les valeurs prédictives positive et négative du test, et interpréter.
Partie B
On rappelle que la probabilité qu'un coyote capturé au hasard présente un test positif est de
- Lorsqu'on capture au hasard cinq coyotes, on assimile ce choix à un tirage avec remise.
On note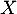 la variable aléatoire qui à un échantillon de cinq coyotes capturés au hasard associe le nombre de coyotes dans cet échantillon ayant un test positif.
la variable aléatoire qui à un échantillon de cinq coyotes capturés au hasard associe le nombre de coyotes dans cet échantillon ayant un test positif.
- Quelle est la loi de probabilité suivie par
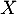 ? Justifier et préciser ses paramètres.
? Justifier et préciser ses paramètres.
- Calculer la probabilité que dans un échantillon de cinq coyotes capturés au hasard, un seul ait un test positif. On arrondira le résultat au centième.
- Un vétérinaire affirme qu'il y a plus d'une chance sur deux qu'au moins quatre coyotes sur cinq aient un test positif : cette affirmation est-elle vraie ? Justifier la réponse.
- Quelle est la loi de probabilité suivie par
- Pour tester des médicaments, les vétérinaires ont besoin de disposer d'un coyote présentant un test positif. Combien doivent-ils capturer de coyotes pour que la probabilité qu'au moins l'un d'entre eux présente un test positif soit supérieure à
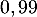 ?
?
Correction
Partie A
Partie B
Cacher la correction
Partie A
-
![\[\psset{xunit=1.3cm,yunit=1.4cm}
\begin{pspicture}(-.4,-2)(4.2,2)
\psline(0,0)(1.5,1)\rput(1.75,1){$M$}
\rput(.8,.9){70\%}
\rput(.8,-1){30\%}
\psline(0,0)(1.5,-1)\rput(1.75,-1){$\overline{M}$}
\psline(2.1,1.2)(3.5,1.6)\rput(3.8,1.6){$T$}
\rput(2.8,1.7){97\%}
\psline(2.1,.8)(3.5,.4)\rput(3.8,.4){$\overline{T}$}
\rput(2.8,.4){3\%}
\rput(2.8,-.4){5\%}
\psline(2.1,-1.2)(3.5,-1.6)\rput(3.8,-1.6){$\overline{T}$}
\psline(2.1,-.8)(3.5,-.4)\rput(3.8,-.4){$T$}
\rput(2.8,-1.7){95\%}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022_c/1.png)
- D'après l'arbre, la probabilité que le coyote soit malade
et que son test soit positif est
![\[P(\overline{M}\cap T)=30\%\tm5\%=1,5\%\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022_c/2.png)
- D'après l'arbre, ou la formule des probabilités totales,
![\[P(T)=70\%\tm97\%+30\%\tm5\%=69,4\%=0,694\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022_c/3.png)
- La valeur prédictive positive du test est la probabilité conditionnelle
![\[P_T(M)=\dfrac{P(M\cap T)}{P(T)}=\dfrac{70\%\tm97\%}{69,4\%}\simeq0,978=97,8\%\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022_c/4.png)
-
- Par analogie avec la question précédente, la « valeur prédictive négative du test » est la probabilité que le coyote ne soit effectivement pas malade sachant que son test est négatif, et vaut
![\[P_{\overline{T}}(\overline{M})=\dfrac{P(\overline{T}\cap\overline{M})}{P(\overline{T})}
=\dfrac{30\%\tm95\%}{1-0,694}\simeq0,931=93,1\%\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022_c/5.png)
- La valeur prédictive positive est plus grande que celle négative: le test est donc plus fiable pour diagonostiquer un animal malade qu'un animal sain.
- Par analogie avec la question précédente, la « valeur prédictive négative du test » est la probabilité que le coyote ne soit effectivement pas malade sachant que son test est négatif, et vaut
Partie B
-
- On répète
 fois l'expérience aléatoire "capturer un coyote",
dont le succès est "le coyote a un test positif" de probabilité
fois l'expérience aléatoire "capturer un coyote",
dont le succès est "le coyote a un test positif" de probabilité
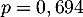 .
Ces répétitions sont identiques et indépendantes (car on l'assimile à un tirage avec remise).
.
Ces répétitions sont identiques et indépendantes (car on l'assimile à un tirage avec remise).
Enfin, la variable aléatoire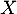 est égale au nombre de succès sur ces 5 répétitions, c'est-à-dire au nombre de coyotes dont le test est positif.
est égale au nombre de succès sur ces 5 répétitions, c'est-à-dire au nombre de coyotes dont le test est positif.
On en déduit que cette variable aléatoire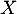 suit la loi binomiale de paramètres
suit la loi binomiale de paramètres
 et
et 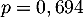 .
.
- La probabilité que dans un échantillon de cinq coyotes capturés au hasard, un seul ait un test positif est, à l'aide de la calculatrice,
![\[P(X=1)\simeq 0,03\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022_c/12.png)
- La probabilité qu'au moins quatre coyotes sur cinq aient un test positif est
![\[P(X\geqslant4)\simeq0,52\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022_c/13.png)
ce qui montre que l'affirmation du vétérinaire est vraie.
- On répète
- On capture donc
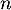 coyotes, et on note
coyotes, et on note 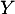 la variable aléatoire égale au
nombre de coyotes ayant un test positif dans cet échantillon.
Comme précédemment,
la variable aléatoire égale au
nombre de coyotes ayant un test positif dans cet échantillon.
Comme précédemment, 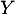 suit la loi binomiale de paramètres
suit la loi binomiale de paramètres 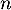 et
et 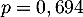 .
.
On cherche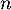 tel que
tel que 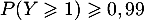
On a
![\[P(Y\geqslant1)=1-P(Y=0)=1-(1-0,694)^n=1-0,306^n\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022_c/21.png)
et donc
![\[\begin{array}{ll}&P(Y\geqslant1)\geqslant0,99\\
\iff& 1-0,306^n\geqslant0,99\\
\iff& 0,306^n\leqslant0,01\enar\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022_c/22.png)
soit, en prenant le logarithme qui est strictement croissant (donc l'ordre est conservé), puis en divisant par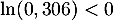 (donc l'ordre est changé):
(donc l'ordre est changé):
![\[\begin{array}{ll}&P(Y\geqslant1)\geqslant0,99\\
\iff&\ln\lp0,306^n\rp=n\ln(0,306)\leqslant\ln(0,01)\\
\iff&n\geqslant\dfrac{\ln(0,01)}{\ln(0,306)}\simeq3,88\enar\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022_c/24.png)
Il faut donc capturer au moins 4 coyote.
Cacher la correction
Tag:Probabilités
Voir aussi:
