Bac 2022 (11 mai): Exponentielle et suite récurrente
Exercice corrigé - Spécialité maths, terminale générale
Dans le cadre d'un essai clinique on envisage deux protocoles de traiterment de
d'une maladie.
L'objectif de cet exercice est d'étudier, pour ces deux protocoles, l'évolution de la quantité de médicament présente dans le sang d'un patient en fonction du temps.
Les parties A et B sont indépendantes
Partie A : Étude du premier protocole
Le premier protocole consiste à faire absorber un médicament, sous forme de comprimé, au patient.
On modélise la quantité de médicament présente dans le sang du patient, exprimée en mg, par la fonction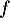 définie sur l'intervalle [0 ; 10] par
définie sur l'intervalle [0 ; 10] par
![\[f(t) = 3t e^{-0,5t+1},\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022/2.png)
où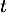 désigne le temps, exprimé en heure, écoulé depuis la prise du comprimé.
désigne le temps, exprimé en heure, écoulé depuis la prise du comprimé.
Partie B : Étude du deuxième protocole
Le deuxième protocole consiste à injecter initialement au patient, par piqüre intraveineuse, une dose de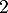 mg de médicament puis à réinjecter toutes les heures une dose de
mg de médicament puis à réinjecter toutes les heures une dose de  mg.
mg.
On suppose que le médicament se diffuse instantanément dans le sang et qu'il est ensuite progressivement éliminé.
On estime que lorsqu'une heure s'est écoulée après une injection, la quantité de médicament dans le sang a diminué de 30 % par rapport à la quantité présente immédiatement après cette injection.
On modélise cette situation à l'aide de la suite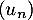 où, pour tout entier naturel
où, pour tout entier naturel 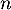 ,
, 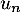 désigne la quantité de médicament, exprimée en mg, présente dans le sang du patient immédiatement après l'injection de la
désigne la quantité de médicament, exprimée en mg, présente dans le sang du patient immédiatement après l'injection de la 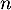 -ième heure. On a donc
-ième heure. On a donc 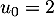 .
.
L'objectif de cet exercice est d'étudier, pour ces deux protocoles, l'évolution de la quantité de médicament présente dans le sang d'un patient en fonction du temps.
Les parties A et B sont indépendantes
Partie A : Étude du premier protocole
Le premier protocole consiste à faire absorber un médicament, sous forme de comprimé, au patient.
On modélise la quantité de médicament présente dans le sang du patient, exprimée en mg, par la fonction
où
-
- On admet que la fonction
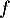 est dérivable sur l'intervalle [0 ; 10] et on note
est dérivable sur l'intervalle [0 ; 10] et on note 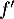 sa fonction dérivée.
Montrer que, pour tout nombre réel
sa fonction dérivée.
Montrer que, pour tout nombre réel 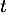 de [0 ; 10], on a:
de [0 ; 10], on a: 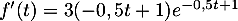 .
.
- En déduire le tableau de variations de la fonction
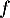 sur l'intervalle [0 ; 10].
sur l'intervalle [0 ; 10].
- Selon cette modélisation, au bout de combien de temps la quantité de médicament présente dans le sang du patient sera-t-elle maximale ? Quelle est alors cette quantité maximale?
- On admet que la fonction
-
- Montrer que l'équation
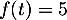 admet une unique solution sur l'intervalle [0 ; 2] notée
admet une unique solution sur l'intervalle [0 ; 2] notée 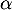 , dont on donnera une valeur approchée à
, dont on donnera une valeur approchée à 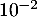 près.
On admet que l'équation
près.
On admet que l'équation 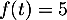 admet une unique solution sur l'intervalle [2 ; 10], notée
admet une unique solution sur l'intervalle [2 ; 10], notée 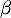 , et qu'une valeur approchée de
, et qu'une valeur approchée de 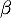 à
à 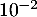 près est 3,46.
près est 3,46.
- On considère que ce traitement est efficace lorsque la quantité de médicament présente dans le sang du patient est supérieure ou égale à 5 mg. Déterminer, à la minute près, la durée d'efficacité du médicament dans le cas de ce protocole.
- Montrer que l'équation
Partie B : Étude du deuxième protocole
Le deuxième protocole consiste à injecter initialement au patient, par piqüre intraveineuse, une dose de
On suppose que le médicament se diffuse instantanément dans le sang et qu'il est ensuite progressivement éliminé.
On estime que lorsqu'une heure s'est écoulée après une injection, la quantité de médicament dans le sang a diminué de 30 % par rapport à la quantité présente immédiatement après cette injection.
On modélise cette situation à l'aide de la suite
- Calculer, selon cette modélisation, la quantité
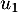 , de médicament (en mg) présente dans le sang du patient immédiatement après l'injection de la première heure.
, de médicament (en mg) présente dans le sang du patient immédiatement après l'injection de la première heure.
- Justifier que, pour tout entier naturel
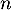 , on a :
, on a : 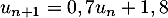 .
.
-
- Montrer par récurrence que, pour tout entier naturel
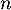 , on a :
, on a : 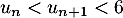 .
.
- En déduire que la suite
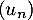 est convergente. On note
est convergente. On note 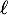 sa limite.
sa limite.
- Déterminer la valeur de
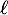 . Interpréter cette valeur dans le contexte de l'exercice.
. Interpréter cette valeur dans le contexte de l'exercice.
- Montrer par récurrence que, pour tout entier naturel
- On considère la suite
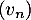 définie, pour tout entier naturel
définie, pour tout entier naturel 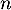 , par
, par 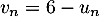 .
.
- Montrer que la suite
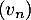 est une suite géométrique de raison
est une suite géométrique de raison 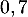 dont on précisera le premier terme.
dont on précisera le premier terme.
- Déterminer l'expression de
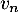 en fonction de
en fonction de 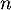 , puis de
, puis de 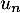 n en fonction de
n en fonction de 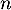 .
.
- Avec ce protocole, on arrête les injections lorsque la quantité de médicament présente dans le sang du patient est supérieure ou égale à 5,5 mg. Déterminer, en détaillant les calculs, le nombre d'injections réalisées en appliquant ce protocole.
- Montrer que la suite
Correction
Partie A : Étude du premier protocole
Partie B : Étude du deuxième protocole
Cacher la correction
Partie A : Étude du premier protocole
-
- On a
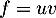 avec
avec 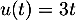 donc
donc 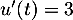 et
et 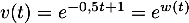 avec
avec
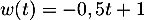 donc
donc 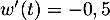 et alors
et alors 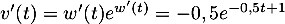 .
.
On obtient alors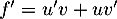 , soit
, soit
![\[\begin{array}{ll}f'(t)&=3e^{-0,5t+1}+3t\tm\lp-0,5e^{-0,5t+1}\rp\\[.4em]
&=3e^{-0,5t+1}\lp1-0,5t\rp\\[.4em]
&=3(-0,5t + 1)e^{-0,5t+1}\enar\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/9.png)
- On a alors le signe de lé dérivée et le sens de variation:
![\[\begin{tabular}{|c|*5c|}\hline
$t$ & 0 && 2 && 10 \\\hline
$-0,5t+1$ && $+$ &\mbox{$0\hspace{-0.67em}\mid$} & $-$ & \\\hline
$e^{-0,5t+1}$ && $+$ &\vline & $+$ & \\\hline
$f'(t)$ && $+$ &\mbox{$0\hspace{-0.67em}\mid$} & $-$ & \\\hline
&&&&&\\
$f$&&\Large{$\nearrow$}&&\Large{$\searrow$}&\\
&&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/10.png)
- Selon cette modélisation, la quantité maximale de médicament présente dans le sang du patient sera de
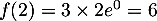 mg, au bout de 2 heures.
mg, au bout de 2 heures.
- On a
-
- Sur [0;2], la fonction
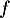 est continue (car même dérivable),
strictement croissante, avec
est continue (car même dérivable),
strictement croissante, avec 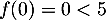 et
et 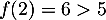 ,
et ainsi, d'après le théorème des valeurs intermédiaires
(théorème de la bijection), on sait donc qu'il existe une unique
solution
,
et ainsi, d'après le théorème des valeurs intermédiaires
(théorème de la bijection), on sait donc qu'il existe une unique
solution 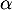 à l'équation
à l'équation 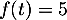 .
.
Avec la calculatrice, par balayage par exemple, on touve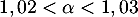 soit,
soit, 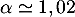 .
.
- On peut compléter le tableau de variation:
![\[\begin{tabular}{|c|*9c|}\hline
$t$ & 0 &&$\alpha$ && 2 &&$\beta$&& 10 \\\hline
&&&&&&&&&\\
$f$&&\psline[arrowsize=8pt]{->}(-.5,-.5)(1.3,.5)&5&&&
\psline[arrowsize=8pt]{->}(-.2,.5)(1.4,-.5)&5&&\\
&&&&&&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/19.png)
grâce auquel on trouve que la durée d'efficacité du médicament est donc de soit 2,44 heures, ou encore 2 heures et 26 minutes.
soit 2,44 heures, ou encore 2 heures et 26 minutes.
- Sur [0;2], la fonction
Partie B : Étude du deuxième protocole
- Selon cette modélisation, à la première heure la quantité dans le sang a diminué de 30%, il en reste donc
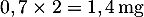 .
On réinjecte de plus une nouvelle dose de 1,8 mg, et on trouve donc que
.
On réinjecte de plus une nouvelle dose de 1,8 mg, et on trouve donc que
![\[u_1=0,7\tm2+1,8=3,2\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/22.png)
- De même que précédemment, à la (n+1)-ème heure,
la quantité dans le sang présente l'heure précédente, soit
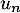 a diminué de 30%, soit
a diminué de 30%, soit 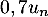 , et on réinjecte, donc ajoute, 1,8 mg.
, et on réinjecte, donc ajoute, 1,8 mg.
On obtient donc bien la relation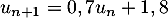 .
.
-
- Soit la proposition
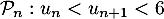 .
.
Initialisation: on a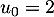 et
et 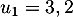 d'où
d'où
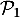 est vraie:
est vraie: 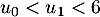 .
.
Hérédité: Supposons que pour un certain entier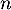 ,
,
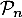 soit vraie, c'est-à-dire
soit vraie, c'est-à-dire
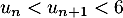 .
.
Alors, en multipliant par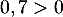 , on obtient
, on obtient
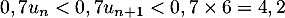 ,
,
puis en ajoutant 1,8 on aboutit à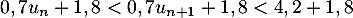 ,
,
c'est-à-dire exactement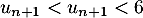 et qui montre donc
et qui montre donc 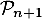 est alors vraie.
est alors vraie.
Conclusion: on vient donc de démontrer, d'après le principe de récurrence, que pour tout entier ,
,
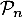 est vraie, c'est-à-dire
est vraie, c'est-à-dire 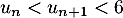 .
.
- On déduit du résultat précédent que la suite
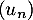 est croissante et aussi qu'elle est majorée par 6.
est croissante et aussi qu'elle est majorée par 6.
On en déduit donc (théorème de convergence monotone) qu'elle converge vers une limite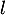 .
.
- On a
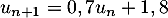 et on sait que
et on sait que  .
.
Ainsi, on doit nécessairement avoir (théorème du point fixe), que
![\[l=0,7l+1,8\iff l=\dfrac{1,8}{0,3}=6\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/46.png)
- Soit la proposition
-
- Pour tout entier
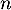 , on a
, on a
![\[\begin{array}{ll}v_{n+1}&=6-u_{n+1}\\
&=6-\lp0,7u_n+1,8\rp\\
&=4,2-0,7u_n\\
&=0,7\lp6-u_n\right)
=0,7v_n\enar\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/48.png)
ce qui montre que la suite est bien géométrique de raison
est bien géométrique de raison 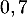 et de premier terme
et de premier terme 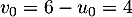 .
.
- On en déduit alors que, pour tout entier
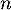 ,
,
![\[v_n=v_0\times q^n=4\times0,7^n\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/53.png)
puis, comme , que
, que
![\[u_n=6-4\tm0,7^n\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/55.png)
- On arrête les injections lorsque la quantité de médicament
présente dans le sang du patient est supérieure ou égale à 5,5 mg,
soit lorsque
![\[\begin{array}{ll}&u_n\geqslant5,5\\
\iff&6-4\tm0,7^n\geqslant5,5\\
\iff&-4\tm0,7^n\geqslant-0,5\enar\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/56.png)
soit, en divisant par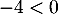 , puis en prenant le logarithme népérien qui est strictement croissant,
, puis en prenant le logarithme népérien qui est strictement croissant,
![\[\begin{array}{ll}&u_n\geqslant5,5\\
\iff&0,7^n\leqslant\dfrac{-0,5}{-4}=0,125\\
\iff&\ln\lp0,7^n\rp=n\ln(0,7)\leqslant\ln(0,125)\enar\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/58.png)
Enfin, en divisant par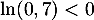 , on obtient finalement
, on obtient finalement
![\[\begin{array}{ll}&u_n\geqslant5,5\\
\iff n\geqslant\dfrac{\ln(0,125)}{\ln(0,7)}\simeq5,8\enar\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/60.png)
Comme on réalise une injection par heure, il faut donc en réaliser 6.
- Pour tout entier
Cacher la correction
Tags:ExponentielleSuites
Voir aussi:
