Bac 2021 (Asie 8 juin): QCM, fonction, suite, python
Exercice corrigé - Spécialité maths, terminale générale
Cet exercice est un questionnaire à choix multiples (QCM)
Pour chaque question, trois affirmations sont proposées, une seule de ces affirmations est exacte.
Le candidat recopiera sur sa copie le numéro de chaque question et la lettre de la réponse choisie pour celle-ci.
Aucune justification n'est demandée. Une réponse fausse ou l'absence de réponse n'enlève aucun point.
Pour chaque question, trois affirmations sont proposées, une seule de ces affirmations est exacte.
Le candidat recopiera sur sa copie le numéro de chaque question et la lettre de la réponse choisie pour celle-ci.
Aucune justification n'est demandée. Une réponse fausse ou l'absence de réponse n'enlève aucun point.
- On considère la fonction
 définie sur
définie sur 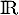 par
par
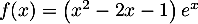 .
.
A. La fonction dérivée de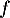 est la fonction définie
par
est la fonction définie
par  .
.
B. La fonction est décroissante sur l'intervalle
est décroissante sur l'intervalle ![$]-\infty~;~2]$](/Generateur-Devoirs/TS/ChapQCM/QCMAsie2021/7.png) .
.
C. .
.
- On considère la fonction
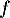 définie sur
définie sur 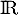 par
par 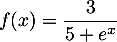 .
Sa courbe représentative dans un repère admet :
.
Sa courbe représentative dans un repère admet :
A. une seule asymptote horizontale;
B. une asymptote horizontale et une asymptote verticale;
C. deux asymptotes horizontales. - On donne ci-dessous la courbe
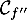 représentant la fonction dérivée seconde
représentant la fonction dérivée seconde 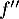 d'une fonction
d'une fonction 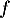 définie et deux fois dérivable sur l'intervalle
définie et deux fois dérivable sur l'intervalle ![$[-3,5~;~6]$](/Generateur-Devoirs/TS/ChapQCM/QCMAsie2021/15.png) .
.
![\[\psset{unit=1cm,arrowsize=7pt 3}
\begin{pspicture}(-4,-3)(7,5)
\psgrid[gridlabels=0pt,subgriddiv=1,gridwidth=0.1pt]
\psaxes[linewidth=1.25pt,labelFontSize=\scriptstyle]{->}(0,0)(-4,-3)(7,5)
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{-3.5}{6}{x 3 exp 0.1 mul x dup mul 0.4 mul sub 1.1 x mul sub 3 add}
\uput[u](6.8,0){$x$} \uput[r](0,4.8){$y$}
\rput[u](1.5,-3.4){Courbe de la fonction d\'eriv\'ee seconde $f''$}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapQCM/QCMAsie2021/16.png)
A. La fonction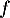 est convexe sur l'intervalle
est convexe sur l'intervalle ![$[-3~;~3]$](/Generateur-Devoirs/TS/ChapQCM/QCMAsie2021/18.png) .
.
B. La fonction admet trois points d'inflexion.
admet trois points d'inflexion.
C. La fonction dérivée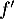 de
de 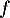 est décroissante sur l'intervalle [0 ; 2].
est décroissante sur l'intervalle [0 ; 2].
- On considère la suite
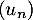 définie pour tout entier naturel
définie pour tout entier naturel 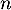 par
par 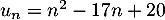 .
.
A. La suite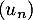 est minorée.
est minorée.
B. La suite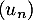 est décroissante.
est décroissante.
C. L'un des termes de la suite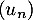 est égal à 2021.
est égal à 2021.
- On considère la suite
 définie par
définie par  et, pour tout entier naturel
et, pour tout entier naturel 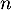 ,
, 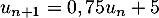 .
.
On considère la fonction « seuil » suivante écrite en Python :
![\[\begin{tabular}{|l|}\hline
def seuil () :\\
\quad u = 2\\
\quad n = 0\\
\quad while u $<$ 45 :\\
\qquad u = 0,75*u + 5\\
\qquad n = n+1\\
\quad return n\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapQCM/QCMAsie2021/32.png)
Cette fonction renvoie :
A. la plus petite valeur de telle que
telle que 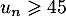 ;
B. la plus petite valeur de
;
B. la plus petite valeur de 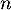 telle que
telle que 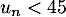 ;
C. la plus grande valeur de
;
C. la plus grande valeur de 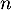 telle que
telle que  .
.
Correction
Cacher la correction
-
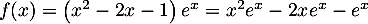 .
.
Comme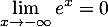 , et que, par croissances comparées,
, et que, par croissances comparées,
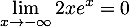 et
et
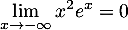 ,
on obtient, par somme de limites:
,
on obtient, par somme de limites:
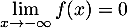 .
.
Réponse C.
- On considère la fonction
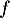 définie sur
définie sur 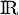 par
par 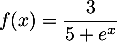 .
.
- On a
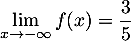 : la droite d'équation
: la droite d'équation 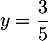 est asymptote horizontale en moins l'infini
est asymptote horizontale en moins l'infini
- On a
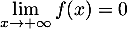 : l'axe des abscisses est asymptote horizontale au voisinage de plus l'infini.
: l'axe des abscisses est asymptote horizontale au voisinage de plus l'infini.
Réponse C.
- On a
- On voit sur la figure que
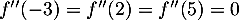 :
la dérivée seconde s'annule trois fois donc la fonction
:
la dérivée seconde s'annule trois fois donc la fonction 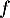 admet
trois points d'inflexion.
Réponse B.
admet
trois points d'inflexion.
Réponse B.
-
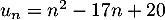 est un trinôme du second degré qui
a un minimum en
est un trinôme du second degré qui
a un minimum en 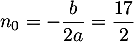 .
.
Le minimum de la suite est donc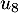 ou
ou 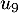 qui est aussi
un minorant de la suite.
Réponse A.
qui est aussi
un minorant de la suite.
Réponse A.
- Réponse A.
Cacher la correction
Tags:QCMFonctionsExponentielleSuites
Voir aussi:
