Bac 2021 - Arbre pondéré, probabilités conditionnelles et loi binomiale
Exercice corrigé - Spécialité maths, terminale générale
Dans une école de statistique, après étude des dossiers des candidats,
le recrutement se fait de deux façons :
On choisit au hasard un candidat à ce concours de recrutement. On notera:
Partie 2
- 10 % des candidats sont sélectionnés sur dossier. Ces candidats doivent ensuite passer un oral à l'issue duquel 60 % d'entre eux sont finalement admis à l'école.
- Les candidats n'ayant pas été sélectionnés sur dossier passent une épreuve écrite à l'issue de laquelle 20 % d'entre eux sont admis à l'école.
On choisit au hasard un candidat à ce concours de recrutement. On notera:
-
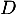 l'évènement « le candidat a été sélectionné sur dossier »;
l'évènement « le candidat a été sélectionné sur dossier »;
-
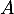 l'évènement « le candidat a été admis à l'école »;
l'évènement « le candidat a été admis à l'école »;
-
 et
et  les évènements contraires des évènements
les évènements contraires des évènements 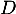 et
et 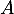 respectivement.
respectivement.
- Traduire la situation par un arbre pondéré.
- Calculer la probabilité que le candidat soit sélectionné sur dossier et admis à l'école.
- Montrer que la probabilité de l'évènement
 est égale à
est égale à  .
.
- On choisit au hasard un candidat admis à l'école. Quelle est la probabilité que son dossier n'ait pas été sélectionné?
Partie 2
- On admet que la probabilité pour un candidat d'être admis à l'école est égale à
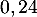 .
.
On considère un échantillon de sept candidats choisis au hasard, en assimilant ce choix à un tirage au sort avec remise. On désigne par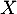 la variable aléatoire dénombrant les candidats admis à l'école parmi les sept tirés au sort.
la variable aléatoire dénombrant les candidats admis à l'école parmi les sept tirés au sort.
- On admet que la variable aléatoire
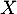 suit une loi binomiale. Quels sont les paramètres de cette loi?
suit une loi binomiale. Quels sont les paramètres de cette loi?
- Calculer la probabilité qu'un seul des sept candidats tirés au sort soit admis à l'école. On donnera une réponse arrondie au centième.
- Calculer la probabilité qu'au moins deux des sept candidats tirés au sort soient admis à cette école. On donnera une réponse arrondie au centième.
- On admet que la variable aléatoire
- Un lycée présente
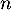 candidats au recrutement dans cette école, où
candidats au recrutement dans cette école, où 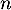 est un entier naturel non nul.
est un entier naturel non nul.
On admet que la probabilité pour un candidat quelconque du lycée d'être admis à l'école est égale à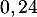 et que les résultats des candidats sont indépendants les uns des autres.
et que les résultats des candidats sont indépendants les uns des autres.
- Donner l'expression, en fonction de
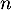 , de la probabilité qu'aucun candidat issu de ce lycée ne soit admis à l'école.
, de la probabilité qu'aucun candidat issu de ce lycée ne soit admis à l'école.
- À partir de quelle valeur de l'entier
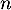 la probabilité qu'au moins un élève de ce lycée soit admis à l'école est-elle supérieure ou égale à
la probabilité qu'au moins un élève de ce lycée soit admis à l'école est-elle supérieure ou égale à 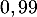 ?
?
- Donner l'expression, en fonction de
Correction
Bac 2021 - 15 mars, sujet 1
Partie 1
Partie 2
Cacher la correction
Bac 2021 - 15 mars, sujet 1
Partie 1
-
![\[\psset{xunit=1.3cm,yunit=.8cm}
\begin{pspicture}(-.4,-2)(4.2,2)
%\rput(0,0){$A_1$}
\psline(0,0)(1.5,1)\rput(1.75,1){$D$}
\rput(.8,.9){0,1}
\rput(.8,-1){0,9}
\psline(0,0)(1.5,-1)\rput(1.75,-1){$\overline{D}$}
\psline(2.1,1.2)(3.5,1.6)\rput(3.8,1.6){$A$}
\rput(2.8,1.7){0,6}
\psline(2.1,.8)(3.5,.4)\rput(3.8,.4){$\overline{A}$}
\rput(2.8,.2){0,4}
\rput(2.8,-.4){0,2}
\psline(2.1,-1.2)(3.5,-1.6)\rput(3.8,-1.6){$\overline{A}$}
\psline(2.1,-.8)(3.5,-.4)\rput(3.8,-.4){$A$}
\rput(2.8,-1.8){0,8}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-1_c/1.png)
- La probabilité que le candidat soit sélectionné sur dossier et admis à l'école est:
![\[P(D\cap A)=0,1\tm0,6=0,06\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-1_c/2.png)
- La probabilité de l'évènement
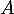 est,
d'après la formule des probabilités totales:
est,
d'après la formule des probabilités totales:
![\[\begin{array}{ll}P(A)
&= P(D\cap A) + P(\overline{D}\cap A) \\
&= 0,06 + 0,9\times 0,2 = 0,24\enar\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-1_c/4.png)
- La probabilité que le dossier n'ait pas été sélectionné,
sachant qu'il a été admis à l'école, est
![\[P_A(\overline{D})
=\dfrac{P(\overline{D}\cap A)}{P(A)}
=\dfrac{0,18}{0,24}=0,75\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-1_c/5.png)
Partie 2
-
- La probabilité du succés, un candidat d'être admis à l'école,
est
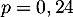 , et on choisit un échantillon de
, et on choisit un échantillon de  candidats.
candidats.
La variable aléatoire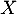 suit donc la loi binomiale
suit donc la loi binomiale
 .
.
- La probabilité qu'un seul des sept candidats tirés au sort soit admis à l'école est:
![\[P(X=1)=\binom{7}{1}\times 0,24^1 \times (1-0,24)^{7-1} \approx 0,32\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-1_c/10.png)
- La probabilité qu'au moins deux des sept candidats tirés au sort
soient admis à cette école est:
![\[P(X\geqslant 2) = 1-P(X\leqslant 1) = 1-0,47=0,53\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-1_c/11.png)
- La probabilité du succés, un candidat d'être admis à l'école,
est
-
- La variable aléatoire
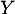 qui donne le nombre d'admis
parmi les
qui donne le nombre d'admis
parmi les 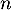 candidats présentés suit la loi binomiale
candidats présentés suit la loi binomiale
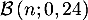 .
La probabilité qu'aucun candidat issu de ce lycée ne soit admis
à l'école est donc
.
La probabilité qu'aucun candidat issu de ce lycée ne soit admis
à l'école est donc
![\[P(Y=0)=\binom{n}{0}\times 0,24^0 \times 0,76^n=0,76^n\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-1_c/15.png)
- On cherche à partir de quelle valeur de l'entier
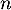 la probabilité
qu'au moins un élève de ce lycée soit admis à l'école est supérieure
ou égale à
la probabilité
qu'au moins un élève de ce lycée soit admis à l'école est supérieure
ou égale à 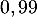 ,
,
![\[\begin{array}{ll}P(Y\geqslant 1) \geqslant 0,99 &\iff 1-P(Y=0) \geqslant 0,99\\
&\iff P(Y=0) \leqslant 0,01\\
&\iff 0,76^n \leqslant 0,01\\
&\iff \ln\left( 0,76^n\right) \leqslant \ln(0,01)\\
&\iff n \times \ln(0,76) \leqslant \ln(0,01)\\
&\iff n \geqslant \dfrac{\ln(0,01)}{\ln(0,76)}\simeq16,8
\enar\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-1_c/18.png)
car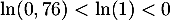 .
.
On trouve donc qu'à partir de 17 élèves la probabilité qu'au moins un élève de ce lycée soit admis à l'école est supérieure ou égale à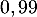 .
.
- La variable aléatoire
Cacher la correction
Tag:Probabilités
Voir aussi:
