Bac 2021 (7 juin): QCM, exponentielle, python
Exercice corrigé - Spécialité maths, terminale générale
Cet exercice est un questionnaire à choix multiples.
Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte.
Une réponse exacte rapporte un point. Une réponse fausse, une réponse multiple ou l'absence de réponse à une question ne rapporte ni n'enlève de point.
Pour répondre, indiquer sur la copie le numéro de la question et la lettre de la réponse choisie.
Aucune justification n'est demandée.
Soit la fonction définie pour tout nombre réel
la fonction définie pour tout nombre réel 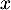 de l'intervalle
de l'intervalle ![$]0~;~ +\infty[$](/Generateur-Devoirs/TS/ChapQCM/QCM2021/3.png) par:
par:
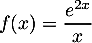 .
.
[.4em] On donne l'expression de la dérivée seconde de
de 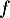 , définie sur l'intervalle
, définie sur l'intervalle ![$]0 ; +\infty[$](/Generateur-Devoirs/TS/ChapQCM/QCM2021/7.png) par:
par:
![\[f''(x)=\dfrac {2e^{2x} (2x^2-2x+1)}{x^3}\]](/Generateur-Devoirs/TS/ChapQCM/QCM2021/8.png)
Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte.
Une réponse exacte rapporte un point. Une réponse fausse, une réponse multiple ou l'absence de réponse à une question ne rapporte ni n'enlève de point.
Pour répondre, indiquer sur la copie le numéro de la question et la lettre de la réponse choisie.
Aucune justification n'est demandée.
Soit
[.4em] On donne l'expression de la dérivée seconde
- La fonction
 , dérivée de
, dérivée de 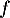 , est définie sur l'intervalle
, est définie sur l'intervalle ![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapQCM/QCM2021/11.png) par:
par:
a.
b.
c.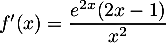
d. .
.
- La fonction
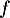 :
:
a. est décroissante sur![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapQCM/QCM2021/17.png) b. est monotone sur
b. est monotone sur ![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapQCM/QCM2021/18.png) c. admet un minimum en
c. admet un minimum en  d. admet un maximum en
d. admet un maximum en  .
.
- La fonction
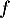 admet pour limite en
admet pour limite en 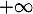 :
:
a.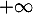
b.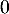
c.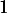
d.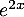 .
.
- La fonction
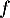 :
:
a. est concave sur![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapQCM/QCM2021/28.png) b. est convexe
b. est convexe ![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapQCM/QCM2021/29.png) c. est concave sur
c. est concave sur ![$\left]0~;~\frac{1}{2}\right]$](/Generateur-Devoirs/TS/ChapQCM/QCM2021/30.png) d. est représentée par une courbe admettant un point d'inflexion
d. est représentée par une courbe admettant un point d'inflexion
- On considère la suite
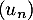 définie par
définie par  et, pour tout entier naturel
et, pour tout entier naturel  ,
,  .
.
On considère la fonction « seuil » suivante écrite en Python :
![\[\begin{tabular}{|l|}\hline
def seuil () :\\
\quad u = 2\\
\quad n = 0\\
\quad while u $<$ 45 :\\
\qquad u = 0,75*u + 5\\
\qquad n = n+1\\
\quad return n\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapQCM/QCM2021/35.png)
Cette fonction renvoie :
a. la plus petite valeur de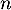 telle que
telle que 
b. la plus petite valeur de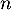 telle que
telle que 
c. la plus grande valeur de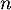 telle que
telle que 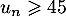 .
.
Correction
QCM - Baccalauréat général, spécialité mathématiques, Métropole 7 juin 2021
Cacher la correction
QCM - Baccalauréat général, spécialité mathématiques, Métropole 7 juin 2021
-
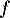 est dérivable comme fonction quotient de fonctions dérivables,
le dénominateur étant non nul sur l'intervalle
est dérivable comme fonction quotient de fonctions dérivables,
le dénominateur étant non nul sur l'intervalle ![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapQCM/QCM2021_c/2.png) , avec
, avec
![\[f'(x) = \dfrac{2e^{2x} \times x - 1 \times e^{2x}}{x^2}
= \dfrac{e^{2x}(2x - 1)}{x^2}\]](/Generateur-Devoirs/TS/ChapQCM/QCM2021_c/3.png)
Réponse c.
- Comme sur l'intervalle
![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapQCM/QCM2021_c/4.png) ,
, 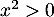 et
et 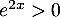 ,
le signe de
,
le signe de 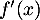 est celui de
est celui de 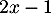 ,
soit
,
soit 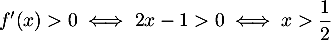 ;
;
et donc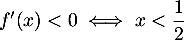 et
et 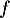 est décroissante sur
est décroissante sur
![$\left]0~;~\frac12\right[$](/Generateur-Devoirs/TS/ChapQCM/QCM2021_c/12.png) ;
et par ailleurs
;
et par ailleurs 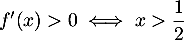 et
et 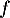 est croissante sur
est croissante sur ![$\left]\frac{1}{2}~;~+ \infty\right[$](/Generateur-Devoirs/TS/ChapQCM/QCM2021_c/15.png) ;
;
On a donc que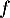 admet un minimum en
admet un minimum en  .
.
Réponse c.
- On a, en posant
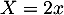 ,
,
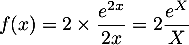 ,et alors
par croissances comparées,
,et alors
par croissances comparées,
![\[\lim_{x \to + \infty}f(x)=\lim_{X \to + \infty}2\dfrac{e^X}{X}=+\infty\]](/Generateur-Devoirs/TS/ChapQCM/QCM2021_c/20.png)
Réponse a.
- Sur
![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapQCM/QCM2021_c/21.png) ,
, 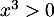 et
et 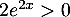 ,
donc le signe de
,
donc le signe de 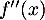 est celui du trinôme
est celui du trinôme 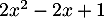 .
.
Le discriminant de ce trinôme est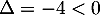 ; il n'admet donc aucune racine,
et il est de signe constant, ici positif, sur
; il n'admet donc aucune racine,
et il est de signe constant, ici positif, sur 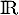 .
.
On en déduit que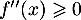 sur
sur ![$]0 ; +\infty[$](/Generateur-Devoirs/TS/ChapQCM/QCM2021_c/29.png) ,
et donc que la fonction y est convexe.
,
et donc que la fonction y est convexe.
Réponse b.
- Réponse a.
Cacher la correction
Tags:QCMFonctionsExponentielle
Voir aussi:
