Bac 2021 (7 juin): Orthogonalité dans l'espace et minimisation d'une distance et volume d'une pyramide
Exercice corrigé - Spécialité maths, terminale générale
Dans un repère orthonormé  on considère
on considère
Le but de cet exercice est de déterminer le point de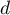 le plus proche du point A et d'étudier quelques propriétés de ce point.
le plus proche du point A et d'étudier quelques propriétés de ce point.
On pourra s'appuyer sur la figure ci-contre pour raisonner au fur et à mesure des questions.
![\[\psset{unit=1.6cm}
\begin{pspicture}(-1.9,-2)(4,2.5)
\psline{->}(-1.7,0)(4,0)
\psline{->}(0,0)(-1,-1.5)
\psline{->}(0,-1.8)(0,2.5)
\rput(-1.2,-1.5){$x$}
\rput(3.95,.2){$y$}
\rput(-.15,2.4){$z$}
\psline(-1,.08)(-1,-.08)\psline(1,.08)(1,-.08)\psline(2,.08)(2,-.08)\psline(3,.08)(3,-.08)
\psline(-.08,-1)(.08,-1)\psline(-.08,1)(.08,1)\psline(-.08,2)(.08,2)
\psline(-.41,-.5)(-.25,-.5)
\psline(-.73,-1)(-.58,-1)
% rep\`ere
\psline[arrowsize=7pt,linewidth=1.2pt]{->}(0,0)(1,0)
\psline[arrowsize=7pt,linewidth=1.2pt]{->}(0,0)(0,1)
\psline[arrowsize=7pt,linewidth=1.2pt]{->}(0,0)(-.35,-.5)
\rput(-.5,-.4){$\vec{i}$}
\rput(-.2,.7){$\vec{k}$}
\rput(.8,.25){$\vec{j}$}
%droite d
\psline(-1,1)(2,-2)\rput(.25,-.5){$\vec{u}$}
\psline[arrowsize=8pt]{->}(0,0)(.5,-.5)
%
\psline(0,0)(2.5,1.5)(2.5,-.5)(1.2,-1.2)
\rput(2.65,1.65){A}
\psline[linestyle=dashed](0,0)(2.5,-.5)
\rput(2.65,-.65){A'}
\psline(2.5,1.5)(1.2,-1.2)
\rput(1,-1.3){$M_0$}
%\psline(-4,-.5)(4,-.5)
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex070621/10.png)
- le point A de coordonnées (1 ; 3 ; 2),
- le vecteur
 de coordonnées
de coordonnées 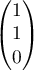
- la droite
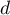 passant par l'origine O du repère et admettant pour vecteur directeur
passant par l'origine O du repère et admettant pour vecteur directeur 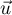 .
.
Le but de cet exercice est de déterminer le point de
On pourra s'appuyer sur la figure ci-contre pour raisonner au fur et à mesure des questions.
![\[\psset{unit=1.6cm}
\begin{pspicture}(-1.9,-2)(4,2.5)
\psline{->}(-1.7,0)(4,0)
\psline{->}(0,0)(-1,-1.5)
\psline{->}(0,-1.8)(0,2.5)
\rput(-1.2,-1.5){$x$}
\rput(3.95,.2){$y$}
\rput(-.15,2.4){$z$}
\psline(-1,.08)(-1,-.08)\psline(1,.08)(1,-.08)\psline(2,.08)(2,-.08)\psline(3,.08)(3,-.08)
\psline(-.08,-1)(.08,-1)\psline(-.08,1)(.08,1)\psline(-.08,2)(.08,2)
\psline(-.41,-.5)(-.25,-.5)
\psline(-.73,-1)(-.58,-1)
% rep\`ere
\psline[arrowsize=7pt,linewidth=1.2pt]{->}(0,0)(1,0)
\psline[arrowsize=7pt,linewidth=1.2pt]{->}(0,0)(0,1)
\psline[arrowsize=7pt,linewidth=1.2pt]{->}(0,0)(-.35,-.5)
\rput(-.5,-.4){$\vec{i}$}
\rput(-.2,.7){$\vec{k}$}
\rput(.8,.25){$\vec{j}$}
%droite d
\psline(-1,1)(2,-2)\rput(.25,-.5){$\vec{u}$}
\psline[arrowsize=8pt]{->}(0,0)(.5,-.5)
%
\psline(0,0)(2.5,1.5)(2.5,-.5)(1.2,-1.2)
\rput(2.65,1.65){A}
\psline[linestyle=dashed](0,0)(2.5,-.5)
\rput(2.65,-.65){A'}
\psline(2.5,1.5)(1.2,-1.2)
\rput(1,-1.3){$M_0$}
%\psline(-4,-.5)(4,-.5)
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex070621/10.png)
- Déterminer une représentation paramétrique de la droite
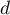 .
.
- Soit
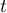 un nombre réel quelconque, et
un nombre réel quelconque, et 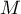 un point de la droite
un point de la droite 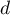 , le point
, le point 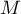 ayant pour coordonnées
ayant pour coordonnées 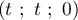 .
.
- On note AM la distance entre les points A et M.
Démontrer que:
![\[AM^2 = 2t^2 - 8t+ 14.\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex070621/19.png)
- Démontrer que le point
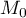 de coordonnées
de coordonnées 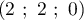 est le point de la droite
est le point de la droite 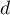 pour lequel la distance
pour lequel la distance 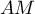 est minimale.
est minimale.
On admettra que la distance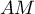 est minimale
lorsque son carré
est minimale
lorsque son carré 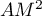 est minimal.
est minimal.
- On note AM la distance entre les points A et M.
Démontrer que:
- Démontrer que les droites
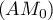 et
et 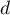 sont orthogonales.
sont orthogonales.
- On appelle
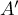 le projeté orthogonal du point
le projeté orthogonal du point 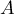 sur le plan
d'équation cartésienne
sur le plan
d'équation cartésienne 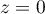 .
Le point
.
Le point 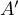 admet donc pour coordonnées
admet donc pour coordonnées 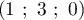 .
.
Démontrer que le point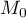 est le point du plan
est le point du plan 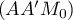 le plus proche du point O, origine du repère.
le plus proche du point O, origine du repère.
- Calculer le volume de la pyramide
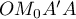 .
.
On rappelle que le volume d'une pyramide est donné par: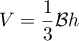 , où
, où 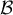 est l'aire
d'une base et
est l'aire
d'une base et 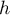 est la hauteur de la pyramide correspondant
à cette base.
est la hauteur de la pyramide correspondant
à cette base.
Correction
(Bac général, spécialité mathématiques, métropole, 7 juin 2021)
Cacher la correction
(Bac général, spécialité mathématiques, métropole, 7 juin 2021)
-
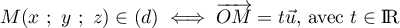 , soit :
, soit :
![\[\left\{\begin{array}{l c l}
x&=&t\\
y&=&t\\
z&=&0
\end{array}\right., \, t \in \R\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex070621_c/2.png)
-
- De
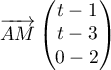 ,
on calcule:
,
on calcule:
![\[\begin{array}{ll}AM^2 &= (t - 1)^2 + (t - 3)^2 + (- 2)^2 \\[.3em]
&= t^2 + 1 - 2t + t^2 + 9 - 6t + 4 \\[.3em]
&= 2t^2 - 8t+ 14\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex070621_c/4.png)
- L'expression précédente est une expression du second degré.
On peut soit étudier les variations (dérivée, signe, ...)
soit se rappeler que le sommet de la parabole est en
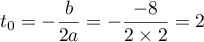 .
.
On a alors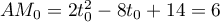 ,
et donc la plus petite distance est
,
et donc la plus petite distance est
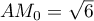 avec
avec 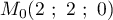 .
.
- De
- On a
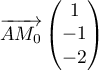 et
et 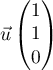 est un vecteur directeur
de
est un vecteur directeur
de 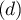 .
.
On a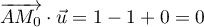 : les vecteurs sont orthogonaux donc les droites
: les vecteurs sont orthogonaux donc les droites 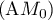 et
et 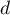 sont orthogonales.
sont orthogonales.
-
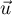 est orthogonal au plan horizontal d'équation
est orthogonal au plan horizontal d'équation 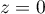 .
Comme A
.
Comme A et
et 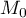 appartiennent à ce plan le vecteur
appartiennent à ce plan le vecteur  est orthogonal au vecteur
est orthogonal au vecteur 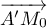 .
.
Donc le vecteur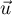 est orthogonal à deux vecteurs non colinéaires
du plan
est orthogonal à deux vecteurs non colinéaires
du plan 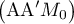 ,donc la droite
,donc la droite 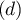 est orthogonale
au plan
est orthogonale
au plan
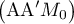 .
Le point
.
Le point 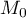 est donc le projeté orthogonal de O
sur le plan
est donc le projeté orthogonal de O
sur le plan 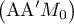 , donc O
, donc O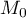 est la distance
la plus courte du point O au plan
est la distance
la plus courte du point O au plan 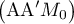 .
.
- On peut prendre la base
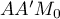 qui est un triangle rectangle en
qui est un triangle rectangle en 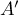 ,
avec
,
avec 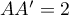
et donc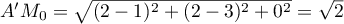 .
.
On a donc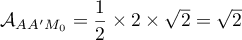 .
.
D'autre part, la hauteur correspondante est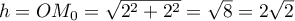 .
.
On obtient finalement
![\[V = \left( AA'M_0\right) = \dfrac{\sqrt2 \times 2\sqrt{2}}{3} = \dfrac43\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex070621_c/35.png)
Cacher la correction
Tag:Géométrie dans l'espace
Voir aussi:
