Bac 2021 (15 mars - sujet 1): Exponentielle et logarithme

Exercice corrigé - Spécialité maths, terminale générale

Soit 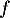$f$ la fonction définie sur l'intervalle $]0~;~ +\infty[$ par :
\[f(x) = \dfrac{e^x}x\]


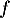On note $\mathcal{C}_f$ la courbe représentative de la fonction $f$ dans un repère orthonormé.


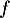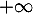    1. Préciser la limite de la fonction $f$ en $+ \infty$.
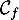    2. Justifier que l'axe des ordonnées est asymptote à la courbe $\mathcal{C}_f$.
  2. Montrer que, pour tout nombre réel 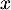$x$ de l'intervalle $]0~;~ +\infty[$, on a :
    \[f'(x)=\dfrac{e^x(x - 1)}{x^2}\]

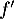    où $f'$ désigne la fonction dérivée de la fonction $f$.
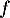  3. Déterminer les variations de la fonction 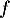$f$ sur l'intervalle $]0~;~ +\infty[$.
    On établira un tableau de variations de la fonction $f$ dans lequel apparaîtront les limites.
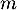  4. Soit $m$ un nombre réel. Préciser, en fonction des valeurs du nombre réel 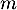$m$, le nombre de solutions de l'équation $f(x) = m$.
  5. On note $\Delta$ la droite d'équation $y = -x$.
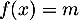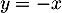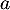    On note A un éventuel point de $\mathcal{C}_f$ d'abscisse $a$ en lequel la tangente à la courbe $\mathcal{C}_f$ est parallèle à la droite $\Delta$.
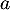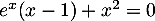    1. Montrer que $a$ est solution de l'équation $e^x(x-1) + x^2 = 0$.


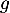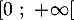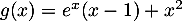      On note $g$ la fonction définie sur $[0~;~ +\infty[$ par $g(x)=e^x(x-1) + x^2 $.
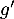      On admet que la fonction $g$ est dérivable et on note $g'$ sa fonction dérivée.
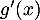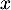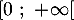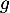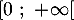    2. Calculer $g'(x)$ pour tout nombre réel $x$ de l'intervalle $[0~;~ +\infty[$, puis dresser le tableau de variations de $g$ sur $[0~;~+\infty[$.
    3. Montrer qu'il existe un unique point $A$ en lequel la tangente à 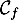$\mathcal{C}_f$ est parallèle à la droite $\Delta$.

Correction
(Bac 15 mars 2021 - sujet 1)
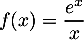Soit $f$ la fonction définie sur l'intervalle $]0~;~ +\infty[$ par : $f(x) = \dfrac{e^x}{x}$.
On note $\mathcal{C}_f$ la courbe représentative de la fonction $f$ dans un repère orthonormé.
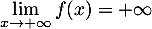    1. D'après le théorème de croissances comparées, on a $\dsp\lim_{x\to+\infty}f(x)=+\infty$.
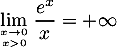    2. On cherche la limite de $f$ en 0. On a $\dsp\lim_{x\to 0} e^{x} = 1$ d'où, par quotient de limites, $\dsp\lim_{x\to 0 \atop x>0} \dfrac{e^x}x=+\infty$, ce qui montre que l'axe des ordonnées est asymptote verticale à la courbe $\mathcal{C}_f$.
  2. Pour tout réel 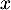$x$ de l'intervalle $]0~;~ +\infty[$, on a, en dérivant le quotient 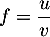$f=\dfrac{u}v$,
    \[f'(x)=\dfrac{e^{x}\times x - e^x\times1}{x^2} = \dfrac{e^x(x-1)}{x^2}\]


  3. On cherche le signe de 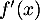$f'(x)$, pour obtenir les variations de $f$,
    \[\renewcommand{\arraystretch}{1.5} \begin{array}{|c | *{6}{c} |} \hline x && 0 & \hspace*{2cm} & 1 & \hspace*{2cm} & +\infty \\ \hline x-1 && & - & \vline\hspace{-2.7pt}{0} & + & \\ \hline e^{x} && & + & \vline\hspace{-2.7pt}{\phantom 0} & + & \\ \hline x^2 & 0& \hfill{} & + & \vline\hspace{-2.7pt}{\phantom 0} & + & \\ \hline f'(x) & \vline\;\vline& & - & \vline\hspace{-2.7pt}{0} &+& \\ \hline & \vline\;\vline\;& +\infty & & & & +\infty \\ f(x) & \vline\;\vline\;& & \psline[arrowsize=8pt]{->}(-1,.6)(1,-.6)& & \psline[arrowsize=8pt]{->}(-1,-.6)(1,.6) & \\ & \vline\;\vline\;& & & e & & \\ \hline \end{array}\]

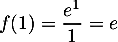
    avec $f(1)=\dfrac{e^{1}}{1}=e$
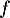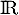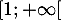  4. D'après le tableau de variations et le théorème des valeurs intermédiaires, $f$ étant continue sur $\R$ et strictement décroissante sur $]0;1[$ et strictement croissante sur $[1;+\infty[$, on a
    • si $m<e$, l'équation $f(x)=m$ n'admet pas de solution;
    • si 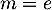$m=e$, l'équation 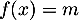$f(x)=m$ admet une solution unique $x=1$;
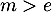    • si $m>e$, l'équation 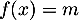$f(x)=m$ admet deux solutions.

    1. La tangente en 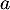$a$ est parallèle à la droite $\Delta$ si et seulement si le coefficient directeur de la tangente est égal à 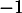$-1$, autrement dit quand 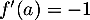$f'(a)=-1$, et donc
      \[\begin{array}{ll}f'(a)=-1 &\iff \dfrac{e^a(a-1)}{a^2}=-1\\ &\iff e^a(x-1) = -a^2\\ &\iff e^{a}(x-1)+a^2=0 \enar\]


      ce qui veut dire que le nombre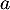 $a$ est solution de l'équation $e^x(x - 1) + x^2 = 0$.
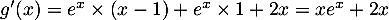
    2. $g'(x)= e^x\times (x-1) + e^x\times 1 + 2x = xe^x+2x$
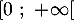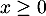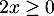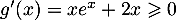      Sur $[0~;~+\infty[$ on a $x\geq0$ et $2x\geq0$ ainsi que $e^x>0$ d'où $g'(x)=xe^{x}+2x \geqslant 0$.
      On dresse alors le tableau de variations

      \[ {\renewcommand{\arraystretch}{1.3} \begin{array}{|c| *3{c}|} \hline x & 0 & \hspace*{2cm} & +\infty \\ \hline g'(x) & 0 &+& \\ \hline & & &\\ g(x) & & \psline[arrowsize=8pt]{->}(-1,-.6)(1,.6) & \\ & -1 & & \\ \hline \end{array} } \]


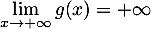    3. On a, comme $\dsp\lim_{x\to+\infty}e^x=+\infty$ et par produit et somme de limite, $\dsp\lim_{x\to+\infty}g(x)=+\infty$.
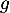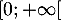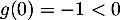      Ainsi, comme $g$ est continue sur $[0;+\infty[$, strictement croissante, et que $g(0)=-1<0$ et avec la limite précédente, on a, d'après le téorème de la bijection (ou théorème des valeurs intermédiaires), qu'il existe une unique solution $a$ à l'équation $g(x)=0$, et donc il existe un unique point A en lequel la tangente à $\mathcal{C}_f$ est parallèle à la droite $\Delta$.


Cacher la correction


Tags:LogarithmeExponentielle

Autres sujets au hasard: Lancer de dés

Voir aussi:
LongPage: h2: 1 - h3: 0