Bac 2009 (Antilles-Guyane): Équation différentielle, exponentielle, suite
Exercice corrigé - Spécialité maths, terminale générale
La température de refroidissement d'un objet fabriqué industriellement
est une fonction  du temps
du temps 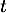 .
Cette fonction
.
Cette fonction 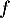 est définie sur l'ensemble des nombres réels positifs et vérifie
l'équation différentielle:
est définie sur l'ensemble des nombres réels positifs et vérifie
l'équation différentielle:
![\[y'(t)+\dfrac12y(t)=10\]](/Generateur-Devoirs/TS/ChapEqDiff/exAG2009/4.png)
La température est exprimée en degrés Celsius ( C)
et le temps
C)
et le temps 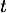 en heures.
en heures.
La température est exprimée en degrés Celsius (
- Déterminer
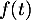 pour
pour  , sachant que pour
, sachant que pour  ,
la température de l'objet est 220
,
la température de l'objet est 220  C.
C.
- Pour la suite, on prendra comme fonction
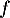 ,
la fonction suivante définie sur
,
la fonction suivante définie sur  par
par
![\[f(t)=200e^{-\frac{t}2}+20\]](/Generateur-Devoirs/TS/ChapEqDiff/exAG2009/13.png)
On note sa courbe représentative.
sa courbe représentative.
- Étudier les variations de la fonction
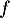 sur
sur 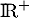 .
.
- Étudier la limite de la fonction
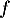 en
en 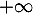 .
La courbe
.
La courbe 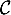 admet-elle une asymptote en
admet-elle une asymptote en 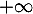 ?
?
- Représenter graphiquement
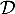 .
.
- Étudier les variations de la fonction
- Déterminer le moment où la température de l'objet est 50
 C.
C.
Donner une valeur approchée de ce moment en heures et minutes.
Correction
D'après Bac S, Antilles-Guyane, 23 juin 2009
Cacher la correction
D'après Bac S, Antilles-Guyane, 23 juin 2009
- Les solutions de l'équation différentielle:
sont
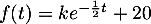 , pour tout réel
, pour tout réel 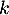 .
.
On sait de plus que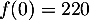 ,
soit
,
soit 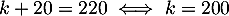 .
.
Ainsi, la température de l'objet est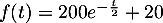 .
.
-
- Comme
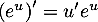 ,
on a
,
on a
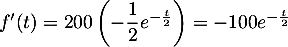 .
Comme
.
Comme 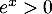 pour tout réel
pour tout réel 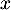 , on trouve donc
que
, on trouve donc
que 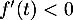 et donc que
et donc que 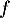 est strictement décroissante.
est strictement décroissante.
- On a
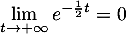 et
donc
et
donc 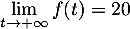 ,
et donc la droite d'équation
,
et donc la droite d'équation 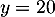 est asymptote
en
est asymptote
en 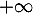 à
à 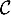 .
.
-
![\[\psset{xunit=1cm,yunit=.02cm,arrowsize=8pt}
\begin{pspicture}(-1,-20)(10,280)
\psline{->}(-.5,0)(8,0)
\psline{->}(0,-5)(0,280)
\psplot[linecolor=blue]{0}{8}{200 2.718 -.5 x mul exp mul 20 add}
\rput(1.3,150){\blue$\mathcal{C}$}
\psline(-.1,20)(8,20)
\rput(1.3,32){$\mathcal{D}$}
\rput[r](-.2,21){$20$}
\rput[r](-.2,220){$220$}
\multido{\i=1+1}{7}{\psline(\i,-5)(\i,5)\rput(\i,-15){\i}}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapEqDiff/exAG2009_c/17.png)
- Comme
- Le moment
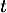 où la température de l'objet est 50
où la température de l'objet est 50  C
est
C
est
![\[\begin{array}{lcl}
&&f(t)=200e^{-\frac{t}2}+20=50\\[1em]
&\iff&
e^{-\frac{t}2}=\dfrac{30}{200}=\dfrac{3}{20}\\[1em]
&\iff&
-\dfrac{t}2=\ln\lp\dfrac3{20}\rp\\[1em]
&\iff&
t=-2\ln\lp\dfrac3{20}\rp\simeq3,8\enar\]](/Generateur-Devoirs/TS/ChapEqDiff/exAG2009_c/20.png)
soit environ 3 heures et 48 minutes.
Cacher la correction
Tag:Équations différentielles
Voir aussi:
