Bac 2008 (La Réunion) - Suite récurrente, somme des termes d'une suite arithmétique, récurrence
Exercice corrigé - Spécialité maths, terminale générale
On considère la suite 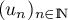 définie par:
définie par:
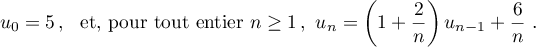
-
- Calculer
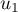 .
.
- Les valeurs de
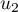 ,
, 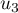 ,
, 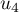 ,
, 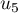 ,
, 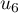 ,
, 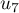 ,
,
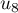 ,
, 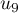 ,
, 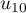 ,
, 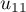 sont respectivement égales à:
sont respectivement égales à:
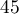 ,
, 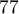 ,
, 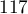 ,
, 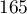 ,
, 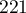 ,
, 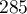 ,
, 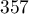 ,
, 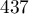 ,
, 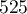 ,
,
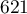 .
.
A partir de ces données, conjecturer la nature de la suite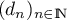 définie par
définie par 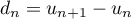 .
.
- Calculer
- On considère la suite arithmétique
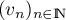 de
raison
de
raison 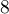 et de premier terme
et de premier terme 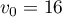 .
.
Justifier que la somme des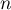 premiers termes de cette suite est
égale à
premiers termes de cette suite est
égale à 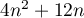 .
.
- Démontrer par récurrence que, pour tout entier naturel
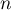 ,
on a:
,
on a:
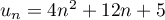
- Valider la conjecture émise à la question 1.b).
Correction
(Baccalauréat La Réunion, juin 2008, 5 points)
Cacher la correction
(Baccalauréat La Réunion, juin 2008, 5 points)
-
-
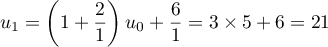 .
.
-
Les premiers termes de la suite
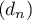 sont:
sont:
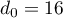 ,
, 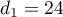 ,
, 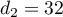 ,
, 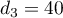 ,
, 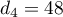 ,
, 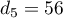 .
A partir de ces premiers termes, on peut conjecturer que
.
A partir de ces premiers termes, on peut conjecturer que 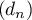 est une suite artithmétique de raison
est une suite artithmétique de raison 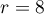 et de premier terme
et de premier terme
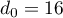 .
.
-
- La somme des
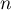 premiers termes de la suite arithmétique
premiers termes de la suite arithmétique
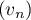 est:
est:
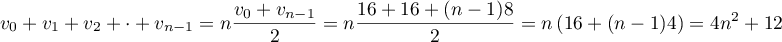 .
.
- Initialisation: pour
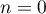 ,
, 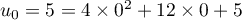 ,
donc la relation est vraie pour
,
donc la relation est vraie pour 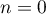 .
Hérédité: Supposons que pour un certain entier
.
Hérédité: Supposons que pour un certain entier 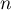 ,
,
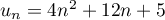 , alors,
, alors,
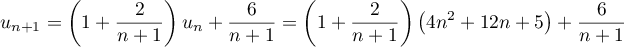 , d'après l'hypothèse de récurrence, et donc,
, d'après l'hypothèse de récurrence, et donc,
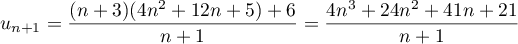 or,
or,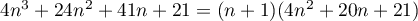 ,
d'où,
,
d'où, 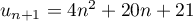 .
.
De plus,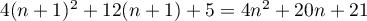 ,
et donc,
,
et donc, 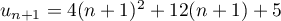 , ce qui montre que
l'expression est encore vraie au rang
, ce qui montre que
l'expression est encore vraie au rang 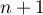 .
.
Conclusion: On vient donc de montrer que, d'après le principe de récurrence, pour tout entier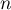 ,
, 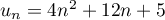 .
.
- Pour tout entier
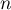 ,
,
![$d_n=u_{n+1}-u_n=
\Big[4(n+1)^2+12(n+1)+5\Big]-\Big[4n^2+12n+5\Big]](/Generateur-Devoirs/TS/ChapSuites/ex108.Reunion_c/30.png) ,
soit
,
soit ![$d_n=\Big[4n^2+20n+21\Big]-\Big[4n^2+12n+5\Big]
=8n+16](/Generateur-Devoirs/TS/ChapSuites/ex108.Reunion_c/31.png) , qui est bien l'expression d'une suite arithmétique de
raison 8 et de premier terme
, qui est bien l'expression d'une suite arithmétique de
raison 8 et de premier terme 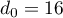 .
.
Cacher la correction
Tag:Suites
Voir aussi:
