Convexité de la fonction exponentielle
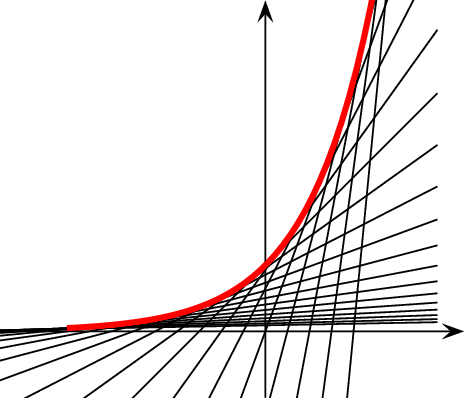
Une fonction f définie et dérivable sur un intervalle I est convexe
lorsque sa courbe est au-dessus de toutes ses tangentes.
Par exemple, pour la parabole (voir la démonstration) de la fonction carré:
![\[\psset{xunit=1.5cm,yunit=1cm,arrowsize=8pt}
\begin{pspicture*}(-3.5,-1)(3.5,5)
\psline{->}(-3,0)(3,0)\psline{->}(0,-1)(0,5)
\newcommand{\ff}[1]{#1 2 div}
\multido{\i=-8+1}{16}{\psplot{-5}{3}{\ff{\i} 2 mul x \ff{\i} sub mul \ff{\i} 2 exp add}}
\psplot[linecolor=red,linewidth=2.5pt]{-3}{2.5}{x 2 exp}
\end{pspicture*}\]](Convexite-exponentielle-IMG/3.png)
Exercice:
On considère la fonction exponentielle f (x) = exp(x) et on note Cf sa courbe représentative.
- Donner l'équation de la tangente Ta à Cf au point d'abscisse a.
- Étudier la position relative de Cf par rapport à Ta.
En déduire que la fonction exponentielle est convexe.
Solution:
- L'équation de la tangente est
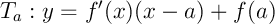 ,
soit, avec
,
soit, avec 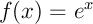 et donc aussi
et donc aussi 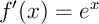 ,
,
![\[T_a: y=e^a(x-a)+e^a\]](Convexite-exponentielle-IMG/14.png)
- D'une manière générale, on étudie la position relative des courbes
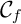 et
et 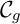 représentatives des courbes
représentatives des courbes 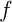 et
et  en étudiant le signe de la différence
en étudiant le signe de la différence 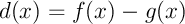 .
.
Ici, on étudie le signe de
![\[\begin{array}{ll}
d(x)&=f(x)-y\\
&=e^x-\left( e^a(x-a)+e^a\rp\\
&=e^x-e^a\left( x-a\rp-e^a
\end{array}\]](Convexite-exponentielle-IMG/20.png)
Pour étudier ce signe, on peut penser à étudier la fonction (dérivée, variations ...)
On a, pour tout réel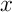 ,
,
![\[d(x)=e^x-xe^x+ae^a-e^a\]](Convexite-exponentielle-IMG/22.png)
et donc,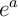 étant une constante (donc de dérivée nulle),
étant une constante (donc de dérivée nulle),
![\[d'(x)=e^x-e^a\]](Convexite-exponentielle-IMG/24.png)
On a alors,
![\[\begin{array}{ll}
d'(x)>0&\iff e^x>e^a\\
&\iff x>a\end{array}\]](Convexite-exponentielle-IMG/25.png)
car la fonction exponentielle est strictement croissante sur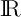 .
.
On obtient donc le tableau de variations:
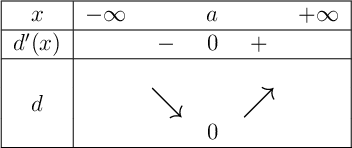
avec .
.
On trouve donc que pour tout réel
pour tout réel 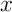 , et donc
que
, et donc
que 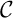 est au-dessus de sa tangente
est au-dessus de sa tangente 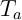 .
.
Ceci étant valable pour un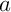 quelconque, on vient ainsi de montrer
que
quelconque, on vient ainsi de montrer
que 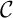 est toujours au-dessus de toutes ses tangentes,
c'est-à-dire que la fonction exponentielle est convexe.
est toujours au-dessus de toutes ses tangentes,
c'est-à-dire que la fonction exponentielle est convexe.
Voir aussi: