Convexité de la fonction carré


Une fonction 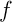$f$ définie et dérivable sur un intervalle 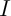$I$ est convexe lorsque sa courbe est au-dessus de toutes ses tangentes.

Par exemple, pour la parabole de la fonction carré:
\[\psset{xunit=1.5cm,yunit=1cm,arrowsize=8pt} \begin{pspicture*}(-3.5,-1)(3.5,5) \psline{->}(-3,0)(3,0)\psline{->}(0,-1)(0,5) \newcommand{\ff}[1]{#1 2 div} \multido{\i=-8+1}{16}{\psplot{-5}{3}{\ff{\i} 2 mul x \ff{\i} sub mul \ff{\i} 2 exp add}} \psplot[linecolor=red,linewidth=2.5pt]{-3}{2.5}{x 2 exp} \end{pspicture*}\]

Le but de l'exercice suivant est justement de démontrer cette propriété de convexité.


Exercice: On considère la fonction carré 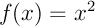$f(x)=x^2$ et on note 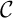$\mathcal{C}$ sa courbe représentative.
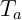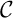  1. Donner l'équation de la tangente $T_a$ à $\mathcal{C}$ au point d'abscisse $a$.
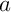  2. Étudier la position relative de 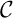$\mathcal{C}$ par rapport à $T_a$.
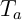    En déduire que la fonction carré est convexe.


Voir aussi:
LongPage: h2: 0 - h3: 0