Exercice corrigé bac 2014 - Suite de nombres complexes
Suite de nombres complexes
Exercice corrigé de mathématiques: Exercice corrigé Bac: suite de nombres complexes, algorithmique
Exercice - énoncé:
Bac S, 8 avril 2014, Pondichéry, 5 points
Le plan complexe est muni d'un repère orthonormé .
Pour tout entier naturel
.
Pour tout entier naturel 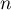 , on note
, on note  le point d'affixe
le point d'affixe  défini par :
défini par :

On définit la suite par
par
 pour tout entier naturel
pour tout entier naturel  .
.

Pour tout entier naturel , on note
, on note  le point d'affixe
le point d'affixe  défini par :
défini par :
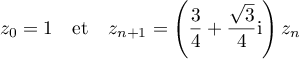
On définit la suite par
par
 pour tout entier naturel
pour tout entier naturel  .
.

Cacher la correction
Le plan complexe est muni d'un repère orthonormé

On définit la suite
- Donner la forme exponentielle du nombre complexe
 .
.
-
- Montrer que la suite
 est géométrique de raison
est géométrique de raison
 .
.
- En déduire l'expression de
 en fonction de
en fonction de  .
.
- Que dire de la longueur O
 lorsque
lorsque  tend vers
tend vers  ?
?
- Montrer que la suite
- On considère l'algorithme suivant :

- Quelle est la valeur affichée par l'algorithme pour
 ?
?
- Pour
 on obtient
on obtient  . Quel est le rôle de cet algorithme ?
. Quel est le rôle de cet algorithme ?
- Quelle est la valeur affichée par l'algorithme pour
-
- Démontrer que le triangle O
 est rectangle en
est rectangle en  .
.
- On admet que
 .
Déterminer les valeurs de
.
Déterminer les valeurs de  pour lesquelles
pour lesquelles  est un point
de l'axe des ordonnées.
est un point
de l'axe des ordonnées.
- Compléter la figure donnée en annexe, à rendre avec la copie,
en représentant les points
 et
et  .
Les traits de construction seront apparents.
.
Les traits de construction seront apparents.
- Démontrer que le triangle O

Correction exercice
Pour tout entier naturel
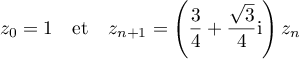
On définit la suite
-

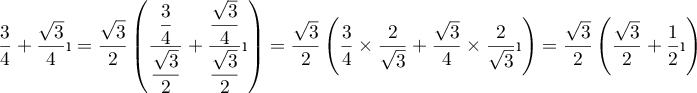
Or et
et 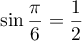 .
.
Donc le nombre complexe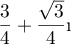 a
pour module
a
pour module  et pour argument
et pour argument 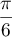 donc sa forme exponentielle est
donc sa forme exponentielle est  .
.
-
-

Donc la suite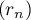 est géométrique de raison
est géométrique de raison  et de premier terme
et de premier terme  .
.
- La suite
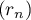 est géométrique donc, pour tout
est géométrique donc, pour tout  ,
,
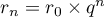 , donc
, donc 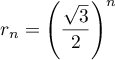 .
.
-

 est une suite géométrique de raison
est une suite géométrique de raison
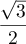 ; or
; or  donc la suite
donc la suite  converge vers 0.
La longueur
converge vers 0.
La longueur 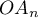 tend donc vers 0 quand
tend donc vers 0 quand  tend vers
tend vers 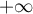 .
.
-
-
- On fait tourner l'algorithme donné dans le texte en prenant pour
 la valeur
la valeur  :
:
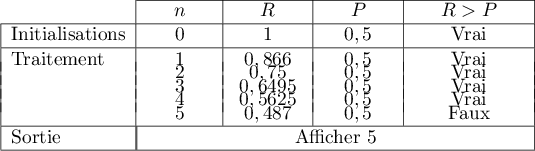
La valeur affichée par l'algorithme pour est 5.
est 5.
- Cet algorithme s'arrête dès que
 et affiche alors
et affiche alors  ,
c'est-à-dire qu'il affiche la plus petite valeur de
,
c'est-à-dire qu'il affiche la plus petite valeur de 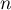 pour
laquelle
pour
laquelle 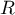 donc
donc 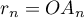 est inférieur ou égal à
est inférieur ou égal à  .
.
On peut donc dire que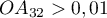 et que
et que  .
Vérification à la calculatrice:
.
Vérification à la calculatrice:
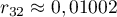 et
et  .
.
- On fait tourner l'algorithme donné dans le texte en prenant pour
-
- On considère le triangle
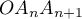 .
.
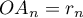 donc
donc 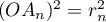
 donc
donc 

 donc
donc 

D'après la réciproque du théorème de Pythagore, le triangle est rectangle en
est rectangle en 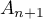 .
.
- On admet que
 .
Le point
.
Le point  , d'affixe
, d'affixe  , appartient à l'axe des ordonnées si
et seulement si son argument est
, appartient à l'axe des ordonnées si
et seulement si son argument est  ou
ou
 modulo
modulo  , c'est-à-dire
, c'est-à-dire  modulo
modulo  , donc il peut s'écrire
, donc il peut s'écrire 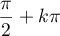 où
où  .
.
Le nombre a pour argument
a pour argument 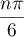 ;
;
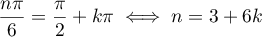 .
.
Mais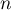 est un entier naturel donc
est un entier naturel donc 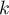 doit être strictement positif donc appartenir à
doit être strictement positif donc appartenir à  .
Donc si
.
Donc si 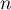 s'écrit
s'écrit  avec
avec  , alors le point
, alors le point 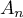 appartient à l'axe des ordonnées.
appartient à l'axe des ordonnées.
- Le point
 a pour affixe
a pour affixe 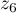 qui a pour argument
qui a pour argument
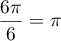 ; ce point est donc sur l'axe des abscisses.
Comme le triangle
; ce point est donc sur l'axe des abscisses.
Comme le triangle  est rectangle en
est rectangle en  , on trace le
cercle de diamètre
, on trace le
cercle de diamètre 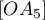 ; le point
; le point  est à
l'intersection de ce cercle et de l'axe des abscisses.
est à
l'intersection de ce cercle et de l'axe des abscisses.
Le point a pour affixe
a pour affixe  qui a pour argument
qui a pour argument
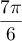 ; donc les points
; donc les points  ,
,  et
et 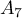 sont
alignés. Le point
sont
alignés. Le point  se trouve donc à l'intersection du cercle de
diamètre
se trouve donc à l'intersection du cercle de
diamètre 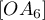 et de la droite
et de la droite  .
.
Etc. (Voir figure)
Remarque: les points et
et 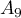 appartiennent à l'axe des
ordonnées, ce qui correspond bien à la réponse trouvée à la question
4.b.
appartiennent à l'axe des
ordonnées, ce qui correspond bien à la réponse trouvée à la question
4.b.
- On considère le triangle

Cacher la correction
Voir aussi: