Exercice corrigé bac S, Nouvelle Calédonie 2015 - Analyse: étude de fonctions avec un paramètre et exponentielle
Fonction avec un paramètre et une exponentielle
Exercice corrigé de mathématiques: Exercice corrigé bac S, Nouvelle Calédonie 2015 - Analyse: étude de fonctions avec un paramètre et exponentielle
Exercice - énoncé:
Le plan est rapporté à un repère orthogonal 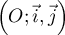 .
.
Soit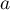 un nombre réel strictement positif.
un nombre réel strictement positif.
On note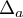 la droite d'équation
la droite d'équation 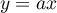 et
et  la courbe représentative de la fonction exponentielle dans le repère orthogonal
la courbe représentative de la fonction exponentielle dans le repère orthogonal 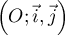 .
.
Le but de cet exercice est de déterminer le nombre de points d'intersection de et
et  suivant les valeurs de
suivant les valeurs de 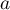 .
.
Pour cela. on considère la fonction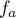 définie pour tout nombre réel
définie pour tout nombre réel 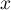 par
par
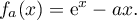
On admet pour tout réel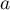 que la fonction
que la fonction 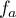 est dérivable sur l'ensemble
est dérivable sur l'ensemble  des nombres réels.
des nombres réels.
![\psset{xunit=3cm,yunit=1.5cm}
\begin{pspicture*}(-1,-0.4)(2,5)
\psaxes[linewidth=1.25pt]{->}(0,0)(-1,-0.4)(2,5)
\psplot[plotpoints=2000,linewidth=1.6pt,linecolor=green]{-1}{2}{x 2 mul}
\psplot[plotpoints=2000,linewidth=1.6pt,linecolor=red]{-1}{2}{x 2.71828 mul}
\psplot[plotpoints=2000,linewidth=1.6pt,linecolor=cyan]{-1}{2}{x 3 mul}
\psplot[plotpoints=2000,linewidth=1.6pt,linecolor=blue]{-1}{2}{2.71828 x exp }
\rput{45}(1.8,3.4){\green $y = 2x$}
\rput{53}(1.8,4.6){\red $y = \text{e}x$}
\rput{57}(1,3.2){\cyan $y = 3x$}
\rput(-0.5,0.75){\blue $\Gamma$}
\uput[ul](0,0){O}
\end{pspicture*}](/Generateur-Devoirs/TS/ChapExponentielle/ex115-NC_c/71.png)
Cacher la correction
Soit
On note
Le but de cet exercice est de déterminer le nombre de points d'intersection de
Pour cela. on considère la fonction
On admet pour tout réel
- Étude du cas particulier
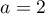 La fonction
La fonction 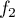 est donc définie pour tout
est donc définie pour tout 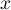 réel par
réel par
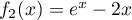 .
.
- Étudier les variations de la fonction
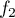 sur
sur 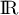 et dresser
son tableau de variations sur
et dresser
son tableau de variations sur  (on ne demande pas de
déterminer les limites aux bornes de l'ensemble de définition.
(on ne demande pas de
déterminer les limites aux bornes de l'ensemble de définition.
- En déduire que
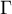 et
et 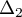 n'ont pas de point
d'intersection.
n'ont pas de point
d'intersection.
- Étudier les variations de la fonction
- Étude du cas général où
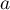 est un réel strictement positif
est un réel strictement positif
- Déterminer les limites de la fonction
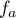 en
en 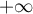 et en
et en
 .
.
- Étudier les variations de la fonction
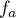 sur
sur  . Montrer
alors que le minimum sur
. Montrer
alors que le minimum sur 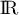 de la fonction
de la fonction  est
est
 .
.
- Étudier le signe de
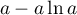 suivant les valeurs du
nombre réel strictement positif
suivant les valeurs du
nombre réel strictement positif 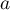 .
.
- Déterminer selon les valeurs du réel
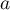 le nombre de points
communs à
le nombre de points
communs à  et
et 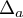 .
.
- Déterminer les limites de la fonction
Correction exercice
-
- D'après l'énoncé la fonction
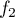 est dérivable sur
est dérivable sur  .
.
On a .
Or
.
Or 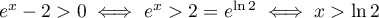 car la fonction
exponentielle est croissante.
On a donc le tableau de variations suivant :
car la fonction
exponentielle est croissante.
On a donc le tableau de variations suivant :
{$x$}\uput[u](1.5,2.4){$- \infty$}\uput[u](4,2.4){$\ln 2$}\uput[u](6.5,2.4){$+ \infty$}
\rput(0.5,2.25){$f'(x)$}\rput(2.5,2.25){$-$} \rput(4,2.25){$0$} \rput(5.5,2.25){$+$}
\rput(0.5,1){$f$}\uput[u](4,0){$2 - 2\ln 2$}
\psline{->}(1.5,1.5)(3.5,0.5)\psline{->}(4.5,0.5)(6.5,1.5)
\end{pspicture}](/Generateur-Devoirs/TS/ChapExponentielle/ex115-NC_c/5.png)
- Comme
 , on en déduit que la fonction est
strictement positive sur
, on en déduit que la fonction est
strictement positive sur 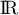 , soit
, soit
 .
.
Ainsi, la courbe représentative de la fonction
exponentielle est toujours strictement au dessus de la droite
représentative de la fonction
exponentielle est toujours strictement au dessus de la droite  .
.
En particulier, et
et 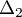 n'ont pas de point commun.
n'ont pas de point commun.
- D'après l'énoncé la fonction
-
-
 En plus l'infini :
En plus l'infini :
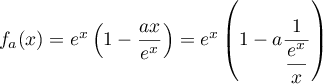 .
.
On sait que, par croissances comparées,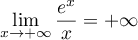 donc
donc
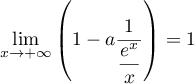 et donc,
comme
et donc,
comme 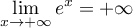 ,
par produit des limites
,
par produit des limites 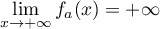 .
.
 En moins l'infini :
En moins l'infini :
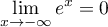 et
et 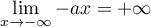 car
car 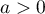 .
Donc, par addtion des limites,
.
Donc, par addtion des limites, 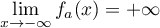 .
.
- D'après l'énoncé,
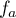 est dérivable sur
est dérivable sur 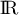 , et on a
, et on a
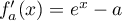 .
.
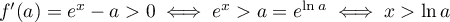 ,
car
,
car  et la fonction exponentielle est strictement croissante.
On a donc le même tableau de variations que pour
et la fonction exponentielle est strictement croissante.
On a donc le même tableau de variations que pour  en
remplaçant 2 par
en
remplaçant 2 par  .
En particulier, la fonction
.
En particulier, la fonction  admet donc un minimum en
admet donc un minimum en 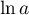 qui est
qui est  .
.
-
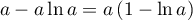 avec
avec 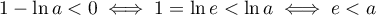 , par croissance de la
fonction logarithme; ainsi:
, par croissance de la
fonction logarithme; ainsi:
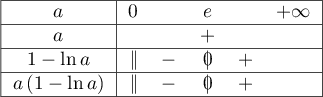
- D'après le tableau de signes précédent qui donne le signe du
minimum de
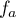 ,
,
 si
si 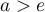 , alors
, alors 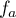 est strictement positive, et donc,
comme en 1),
est strictement positive, et donc,
comme en 1),  et
et 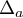 n'ont aucun point
d'intersection.
n'ont aucun point
d'intersection.
 si
si 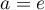 , alors
, alors  , et pour tout
, et pour tout 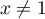
 .
.
 et
et 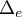 se coupent une unique fois
(
se coupent une unique fois
(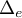 est tangente à
est tangente à 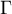 au point
au point 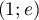 ).
).
 si
si 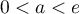 , le minimum de
, le minimum de  est négatif,
est négatif,
{$x$}\uput[u](1.5,2.4){$- \infty$}\uput[u](4,2.4){$\ln a$}\uput[u](6.5,2.4){$+ \infty$}
\uput[u](1.5,1.4){$+\infty$}\uput[u](6.5,1.4){$+\infty$}
\rput(0.5,2.25){$f'(x)$}\rput(2.5,2.25){$-$} \rput(4,2.25){$0$} \rput(5.5,2.25){$+$}
\rput(0.5,1){$f$}\uput[u](4,0){$a - 2\ln a$}
\psline{->}(1.5,1.5)(3.5,0.5)\psline{->}(4.5,0.5)(6.5,1.5)
\end{pspicture}](/Generateur-Devoirs/TS/ChapExponentielle/ex115-NC_c/56.png)
Sur l'intervalle![$]-\infty~;~\ln a[](/Generateur-Devoirs/TS/ChapExponentielle/ex115-NC_c/57.png) ,
la fonction
,
la fonction 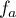 est continue (car dérivable),
strictement décroissante, avec
est continue (car dérivable),
strictement décroissante, avec 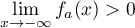 et
et
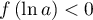 . Ainsi, d'après le théorème de la bijection (ou
corollaire du théorème des valeurs intérmédiaires),
il existe un unique
. Ainsi, d'après le théorème de la bijection (ou
corollaire du théorème des valeurs intérmédiaires),
il existe un unique ![$\alpha\in]-\infty;\ln a[](/Generateur-Devoirs/TS/ChapExponentielle/ex115-NC_c/61.png) tel que
tel que
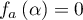
Le même raisonnement est aussi valable sur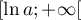 :
il existe un unique
:
il existe un unique ![$\beta\in]\ln a;+\infty[](/Generateur-Devoirs/TS/ChapExponentielle/ex115-NC_c/64.png) tel que
tel que
 .
.
Ainsi, si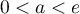 ,
,  et
et  ont deux points
d'intersections distincts (les points de coordonnées
ont deux points
d'intersections distincts (les points de coordonnées
 et
et 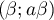 ).
).
-
![\psset{xunit=3cm,yunit=1.5cm}
\begin{pspicture*}(-1,-0.4)(2,5)
\psaxes[linewidth=1.25pt]{->}(0,0)(-1,-0.4)(2,5)
\psplot[plotpoints=2000,linewidth=1.6pt,linecolor=green]{-1}{2}{x 2 mul}
\psplot[plotpoints=2000,linewidth=1.6pt,linecolor=red]{-1}{2}{x 2.71828 mul}
\psplot[plotpoints=2000,linewidth=1.6pt,linecolor=cyan]{-1}{2}{x 3 mul}
\psplot[plotpoints=2000,linewidth=1.6pt,linecolor=blue]{-1}{2}{2.71828 x exp }
\rput{45}(1.8,3.4){\green $y = 2x$}
\rput{53}(1.8,4.6){\red $y = \text{e}x$}
\rput{57}(1,3.2){\cyan $y = 3x$}
\rput(-0.5,0.75){\blue $\Gamma$}
\uput[ul](0,0){O}
\end{pspicture*}](/Generateur-Devoirs/TS/ChapExponentielle/ex115-NC_c/71.png)
Cacher la correction
Voir aussi: