Exercice corrigé type bac sur les suites

Suite récurrente, démonstration par récurrence, et limite d'une suite



Exercice corrigé de mathématiques: Exercice corrigé type Bac: suites, démonstration par récurrence, et limite d'une suite

Exercice - énoncé:

On considère la suite définie par:   et .
  1. Dans cette question, on donne et .
    1. Exprimer la différence , et en déduire le sens de variation de la suite .
    2. Démontrer que, pour tout entier , .
    3. En déduire que la suite converge.
    4. Déterminer la limite de la suite .

  2. Dans cette question, on donne et .
    1. Etudier les variations de la fonction sur et montrer que .
    2. Démontrer par récurrence que, pour tout entier , .
    3. En déduire que la suite converge.
    4. Déterminer la limite de la suite .

Correction exercice


On considère la suite définie par:   et .
  1. Dans cette question, on donne et , soit .
    1. .
      Ainsi, pour tout entier , , soit 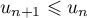, et la suite est donc décroissante.
    2. Démontrons par récurrence la propriété: .
      Initialisation: Pour , , et on a donc bien .
      Hérédité: Supposons que pour un entier , on ait .
      Alors, . Ainsi, comme , on a donc en multipliant ces deux dernières inégalités , soit .
      La propriété est donc encore vraie au rang .
      Conclusion: D'après le principe de récurrence, on a donc, pour tout entier , .
    3. La suite est donc décroissante et minorée par . On en déduit donc qu'elle converge vers une limite .
    4. La limite vérifie nécessairement (point fixe) .
      Ainsi, la suite converge vers .

  2. Dans cette question, on donne et , soit .
    1. Pour tout , .
       
      De plus, .




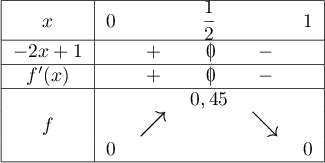
    2. Initialisation: Pour , et . On a bien ainsi . Hérédité: Supposons que pour un entier , on ait .
      Comme la fonction est croissante sur , on a donc .
      Or, , , et .
      Ainsi, , et la propriété est encore vraie au rang .
      Conclusion: D'après le principe de récurrence, pour tout entier , .
    3. La suite est donc croissante est majorée par . On en déduit qu'elle converge vers une limite .
    4. La limite vérifie nécessairement .
      Or est croissante avec , et donc, pour tout entier , .
      La limite de la suite ne peut donc être que .


Cacher la correction


Voir aussi:
ccc